Odchýlka podstavy a bočnej strany
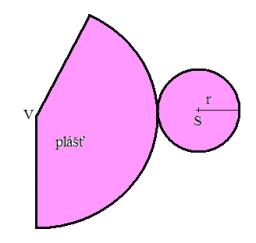
Povrch rotačného kužeľa je 30 cm2, obsah jeho plášťa je 20 cm2. Vypočítajte odchýlku strany tohto kužeľa od roviny podstavy.
Správna odpoveď:
Tipy na súvisiace online kalkulačky
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
algebrastereometriaplanimetriagoniometria a trigonometriaJednotky fyzikálnych veličínÚroveň náročnosti úlohy
Súvisiace a podobné príklady:
- Vypočítaj 349
 Vypočítaj objem a povrch rotačného kužeľa, ak jeho výška je 10 cm a strana má od roviny podstavy odchýlku 30°.
Vypočítaj objem a povrch rotačného kužeľa, ak jeho výška je 10 cm a strana má od roviny podstavy odchýlku 30°. - Kužeľ
 Obsah plášťa kužeľa je 4 cm², obsah podstavy kužeľa je 2 cm². Určte v stupňoch uhol (odchýlku) strany kužeľa a roviny podstavy kužeľa. (Strana kužeľa je úsečka spájajúca vrchol kužeľa s ľubovoľným bodom kružnice podstavy. Všetky strany kužeľa tvoria plášť
Obsah plášťa kužeľa je 4 cm², obsah podstavy kužeľa je 2 cm². Určte v stupňoch uhol (odchýlku) strany kužeľa a roviny podstavy kužeľa. (Strana kužeľa je úsečka spájajúca vrchol kužeľa s ľubovoľným bodom kružnice podstavy. Všetky strany kužeľa tvoria plášť - Strecha veže
 Strecha veže má tvar plášťa rotačného kužeľa s priemerom podstavy 4,3 m. Odchýlka strany od roviny podstavy je 36°. Vypočítajte spotrebu plechu na pokrytie strechy, ak počítame 8 % na odpad.
Strecha veže má tvar plášťa rotačného kužeľa s priemerom podstavy 4,3 m. Odchýlka strany od roviny podstavy je 36°. Vypočítajte spotrebu plechu na pokrytie strechy, ak počítame 8 % na odpad. - Rotačný kužeľ
 Obsah plášta rotačného kužeľa je 240 cm² a obsah jeho podstavy 160 cm². Vypočítaj objem tohto kužeľa.
Obsah plášta rotačného kužeľa je 240 cm² a obsah jeho podstavy 160 cm². Vypočítaj objem tohto kužeľa. - Povrch valca
 Obsah plášťa rotačného valca je trikrát väčší ako obsah jednej podstavy tohto valca. Polomer podstavy valca je 10 cm. Aký je povrch valca?
Obsah plášťa rotačného valca je trikrát väčší ako obsah jednej podstavy tohto valca. Polomer podstavy valca je 10 cm. Aký je povrch valca? - Tienidlo 3
 Tienidlo lampy má tvar plášťa rotačného kužela so stranou 32 cm a priemerom podstavy 46 cm. Vypočítajte spotrebu papiera na jeho výrobu ak predpokladáte, že odpad bude 6%
Tienidlo lampy má tvar plášťa rotačného kužela so stranou 32 cm a priemerom podstavy 46 cm. Vypočítajte spotrebu papiera na jeho výrobu ak predpokladáte, že odpad bude 6% - Kornútok
 Do ktorého z vrecúšok v tvare plášťa rotačného kužeľa sa zmestí väčšie množstvo praženej kukurice? Prvé vrecko má výšku 20 cm a dĺžka jeho strany je 24 cm, druhé vrecko má polomer podstavy 10 cm a výšku 25 cm.
Do ktorého z vrecúšok v tvare plášťa rotačného kužeľa sa zmestí väčšie množstvo praženej kukurice? Prvé vrecko má výšku 20 cm a dĺžka jeho strany je 24 cm, druhé vrecko má polomer podstavy 10 cm a výšku 25 cm.
