Parabolická

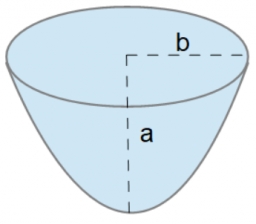
Parabolická úseč má základnu a= 4 cm a výšku v= 6 cm. Vypočítejte objem tělesa, které vznikne rotací této úseče

a) kolem své základny
b) kolem své osy.

Předem děkuji za řešení.

Správná odpověď:

V₁ = 51,2 cm³
V₂ = 50,2655 cm³

Postup správného řešení:

a = 4 cm v = 6 cm f (x) = q x^{2} f (a / 2) = q (a / 2)^{2} = v 6 = q \cdot 2^{2} q = 6 / 2^{2} = \frac{3}{2} = 1, 5 V_{1} = \frac{8}{1 5} \cdot v \cdot a^{2} = \frac{8}{1 5} \cdot 6 \cdot 4^{2} = \frac{2 5 6}{5} cm^{3} = 51, 2 cm^{3}

f (x) = v - \frac{6}{4} x^{2} f (x) = 6 - \frac{6}{4} x^{2} x_{0} = - a / 2 = - 4 / 2 = - 2 x_{1} = a / 2 = 4 / 2 = 2 V_{2} = π \cdot \int_{{} x_{0}}^{{} x_{1}} f (x) d_{x} V_{2} = π \cdot \int_{{} x_{0}}^{{} x_{1}} (\frac{6}{4} x^{2} - v) d_{x} V_{2} = π \cdot [\frac{6}{4} \cdot x^{3} / 3 - v_{x}]_{{} x_{0}}^{{} x_{1}} F (x) = 6 x - \frac{6}{4} \cdot x^{3} / 3 F_{1} = 6 \cdot x_{1} - \frac{6}{4} \cdot x_{1}^{3} / 3 = 6 \cdot 2 - \frac{6}{4} \cdot 2^{3} / 3 = 8 F_{0} = 6 \cdot x_{0} - \frac{6}{4} \cdot x_{0}^{3} / 3 = 6 \cdot (- 2) - \frac{6}{4} \cdot (- 2)^{3} / 3 = - 8 V_{2} = π \cdot (F_{1} - F_{0}) = 3, 1416 \cdot (8 - (- 8)) = 50, 2655 cm^{3}

Našel jsi chybu či nepřesnost? Klidně nám ji napiš.

Zobrazuji 6 komentářů:

Žák

a) Pa = 384/5*pi = cca 241,27 cm³
b) Pb = 12*pi = cca 37,70 cm³

5 let Like

Matematik

b - nie 16 pi ?

5 let Like

Žák

Va = pi*integrate (sqrt(2/3*x)² dx from x=0 to 6
Vb = pi*integrate (-6/4*x²+6)² dx from x=-2 to 2

5 let Like

Aztli

Je to podivně zadané

5 let Like

Aztli

Objem paraboloidu, bude 48 pi, pro kontrolu lze dvěma způsoby buď kolem osy Y z funkce I (2*pi * x * 3/8 * x² dx od nuly do 4) nebo z inverzní funkce I (pi * ((8/3*x)^.5)² dx od nuly do 6. Co je nejvíce pozoruhodné, že to bude přesně polovina objemu válce, který má takto pi * 4² * 6 = 96 pi.

5 let Like

Aztli

Co se týče druhého zadání, tak není zcela jasné, co má rotovat, zda kolem celé základny oblouk paraboly, či jen část. Tedy jen část oblouku paraboly, co je pod z úsečkou b nebo obě části paraboly pod úsečkou 2*b.V podstatě stačí počítat rotaci oblouku paraboly jen části pod úsečkou b, pokud by to mělo jako být pod jejím dvojnásobkem, bude podobně vzhledem k symetrii objem dvojnásobný.Čili můžeme nechat tedy rotovat část oblouku paraboly upravené na tvar y=3/8*x²-6 kolem osy x, pak to bude integral v mezích (0,4) z pi* (3/8*x²-6)² dx = 384/5 pi.
Nebo funkci upravit, aby rotovala kolem osy y, pak bude mít tvar y=(8/3*(6-x))^.5 a pak bude mít integrál tvar : v mezích od 0 do 6 z funkce 2pi * x * (8/3*(6-x))^.5 dx a vyjde opět objem 384/5 * pi (musí se v absolutní hodnotě). Válec, ve kterém je tento objem obsažen má objem pi * 6²*4 = 144pi, co je zajímavé je, že objem bude téměř polovina objemu válce, ale nikoliv přesně, ale nepatrně méně. Pokud by tedy rotoval kolem základny 2 * b, bude příslušný oblouk v prostoru vymezovat dvojnásobný objem v příslušném také dvojnásobné válci.

5 let Like