Parabolický úsek
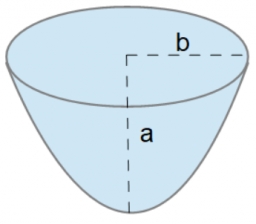
Parabolický úsek má základňu a = 4 cm a výšku v = 6 cm. Vypočítajte objem telesa, ktoré vznikne rotáciou tejto úseče
a) okolo svojej základne
b) okolo svojej osi.
Vopred ďakujem za riešenie.
Vaša odpoveď:
a) okolo svojej základne
b) okolo svojej osi.
Vopred ďakujem za riešenie.
Vaša odpoveď:
Zobrazujem 1 komentár:
Miro
Treba určiť čo je r a čo v. (Ak na Vašom obr. a=¸V; b=R)
V=(1/2)*PI()*R*R*V , ak rotujeme okolo V (P=(2/3)*R*V)
Podľa Guldinovej vety Objem=plocha ktorú rotujeme*dráha ťažiska.
Ťažisko je od vrcholu a teda aj od osi rotácie 3/8R, jeho dráha je 2*pi()*(3/8)*R, a objem je uvedených (1/2)*PI()*R*R*V. Po dosadení V=(1/2)*R*R*V=150,796447cm3
Ak rotujeme okolo R, ťažisko od vrcholu je (3/5)*V, od osi rotácie teda (2/5)*V.
Po dosadení V=(8/15)*R*V*V=241,274316cm3
V=(1/2)*PI()*R*R*V , ak rotujeme okolo V (P=(2/3)*R*V)
Podľa Guldinovej vety Objem=plocha ktorú rotujeme*dráha ťažiska.
Ťažisko je od vrcholu a teda aj od osi rotácie 3/8R, jeho dráha je 2*pi()*(3/8)*R, a objem je uvedených (1/2)*PI()*R*R*V. Po dosadení V=(1/2)*R*R*V=150,796447cm3
Ak rotujeme okolo R, ťažisko od vrcholu je (3/5)*V, od osi rotácie teda (2/5)*V.
Po dosadení V=(8/15)*R*V*V=241,274316cm3
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
algebraaritmetikaplanimetriazákladné operácie a pojmyJednotky fyzikálnych veličínÚroveň náročnosti úlohy
Súvisiace a podobné príklady:
- Vypočítajte 79
Vypočítajte objem kužeľa, ktorý vznikne rotáciou rovnoramenného trojuhol níka okolo výšky na základňu, ak trojuholník má rameno dlhé 15 cm a výšku na základňu 12 cm. Pri výpočte použite hodnotu pi = 3,14 a výsledok zaokrúhlite na jedno desatinné miesto. - Výška valca
Výpočet výšky a polomeru valca Je daný obdĺžnik ABCD |AB| = 8 cm, |BC| = 4 cm. Určte výšku a polomer valca, ktorý vznikne rotáciou obdĺžnika okolo úsečky AB. - Rotácia
Vypočítaj povrch a objem kužeľa, ktorý vznikne rotáciou pravouhlého trojuholníka ABC s odvesnami dlhými 6 cm a 9 cm okolo kratšej odvesny. - Rotačné 8
Rotačné teleso vzniklo rotáciou rovnostranného trojuholníka s dĺžkou strany a=2 cm okolo jednej z jeho strán. Vypočítajte objem tohoto rotačného telesa. - Pravouhlý 35
Pravouhlý trojuholník má odvesny dlhé 3 cm a 4 cm. Jeden kužeľ (nazvime ho A) vznikol rotáciou tohto trojuholníka okolo dlhej odvesny, druhý (označíme B) rotáciou okolo kratšej odvesny. Ktorý kužeľ má: a) väčší objem b) menší plášť c) väčší celý povrch? - Otáčanie štvorca
Štvorec o strane dĺžky 3 cm sa otáča okolo svojej uhlopriečky. Vypočítajte objem a povrch vzniknutého telesa - Rotácia
Pravouhlý trojuholník má strany a = 11 a b = 10. Prepona je c. Ak sa trojuholník otáča okolo strany c ako os, nájdite objem a plochu povrchu kužeľovej plochy vytvorenej touto rotáciou.
