Rotačné 8
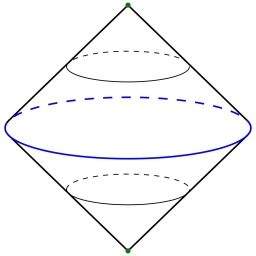
Rotačné teleso vzniklo rotáciou rovnostranného trojuholníka s dĺžkou strany a=2 cm okolo jednej z jeho strán. Vypočítajte objem tohoto rotačného telesa.
Vaša odpoveď:
Vaša odpoveď:
Zobrazujem 1 komentár:
Jana
su to dva rovnake kuzele. s podstavami s polomerom r=sqrt(3) a výškou h=1. To rozdelenie je nutne preto, lebo rotáciou rovnostranného trojuholníka okolo danej osi nevznikne rotačný kužeľ, ale teleso tvorené dvoma rotačnými kužeľmi, spojenými podstavou. V osovom reze - rozdelime rovnostranny trojuholnik vyskou. Ta vyska sa stane polomerom podstavy. Jeden kuzel vznikne rotaciou jedneho pravouhleho trojuholnika, druhy kuzel rotaciou druheho PT.
Tipy na súvisiace online kalkulačky
Tip: premeniť jednotky objemu vám pomôže naša kalkulačka premeny jednotiek objemu.
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
algebraaritmetikastereometriaplanimetriazákladné operácie a pojmyJednotky fyzikálnych veličínÚroveň náročnosti úlohy
Súvisiace a podobné príklady:
- RS trojuholník
Vypočítajte s presnosťou na stotiny cm výšku rovnostranného trojuholníka s dĺžkou strany 12 cm. Vypočítajte jeho obvod a obsah. - Povrch hranola
Vypočítajte povrch a objem kolmého hranola, ak meria jeho výška h = 18 cm a ak je podstavou rovnostranný trojuholník s dĺžkou strany a = 7,5 cm - Rovnostranný - hranol
Vypočítajte objem a povrch hranola s výškou 9,6 cm s podstavou rovnostranného trojuholníka s dĺžkou 4,8 cm. - Vypočítajte kúžeľ
Je daný rotačný kúžeľ s výškou 18 cm a dĺžkou bočnej strany s = 45 cm. Vypočítajte jeho povrch a objem. - Rotácia
Pravouhlý trojuholník má strany a = 11 a b = 10. Prepona je c. Ak sa trojuholník otáča okolo strany c ako os, nájdite objem a plochu povrchu kužeľovej plochy vytvorenej touto rotáciou. - Ruže 3
Kvetinový záhon pred domom má tvar rovnostranného trojuholníka s dĺžkou strany 2,5 m. Mama vysádza po jeho obvode ruže. Koľko kríkov ruží mama potrebuje na vysadenie, keď kríky vysádza v rovnakej vzdialenosti 50 cm od seba. .. - Tri kocky 2
Teleso vzniklo zlepenim troch zhodných kociek. Jeho objem je 192 cm³. Aký je jeho povrch v dm² ?
