Poloměr kružnice
Bod B je střed kružnice. Přímka AC se dotýká kružnic v bodě C a platí AB=20 cm a AC=16 cm. Jaký je poloměr kružnice BC?
Správná odpověď:
Tipy na související online kalkulačky
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
geometrieplanimetrieÚroveň náročnosti úkolu
Doporučujeme k tomuto príkladu si prohlédnout toto výukové video: video1
Související a podobné příklady:
- Sestrojte 4
 Sestrojte trojúhelník ABC: kružnice vepsaná má poloměr r= 2 cm, úhel alfa=50 stupňů, c= 8 cm. Proveďte náčrtek, popis konstrukce a rozbor.
Sestrojte trojúhelník ABC: kružnice vepsaná má poloměr r= 2 cm, úhel alfa=50 stupňů, c= 8 cm. Proveďte náčrtek, popis konstrukce a rozbor. - Tětiva BC
 Je dána kružnice k se středem v bodě S = [0; 0]. Bod A = [40; 30] leží na kružnici k. Jak dlouhá je tětiva BC pokud střed P této tětivy má souřadnice: [- 14; 0]?
Je dána kružnice k se středem v bodě S = [0; 0]. Bod A = [40; 30] leží na kružnici k. Jak dlouhá je tětiva BC pokud střed P této tětivy má souřadnice: [- 14; 0]? - Kružnice
 Kružnice se dotýká dvou rovnoběžek p a q, její střed leží na přímce a, která je sečnou obou přímek. Napište její rovnici a určete souřadnice středu a poloměru. p: -5x-y-1 = 0 q: -5x-y+7 = 0 a: -2x+5y-6 = 0
Kružnice se dotýká dvou rovnoběžek p a q, její střed leží na přímce a, která je sečnou obou přímek. Napište její rovnici a určete souřadnice středu a poloměru. p: -5x-y-1 = 0 q: -5x-y+7 = 0 a: -2x+5y-6 = 0 - Délka úsečky BC
 Body A, B a C jsou kolineární a B leží mezi A a C. Pokud AC = 48, AB = 2x + 2 a BC = 3x + 6, jaká je délka BC?
Body A, B a C jsou kolineární a B leží mezi A a C. Pokud AC = 48, AB = 2x + 2 a BC = 3x + 6, jaká je délka BC? - Sestroj 21
 Sestroj rovnoběžník ABCD: AB=4,8cm, va=3cm, BC =4cm. Vypočítejte obvod. Proveďte náčrtek.
Sestroj rovnoběžník ABCD: AB=4,8cm, va=3cm, BC =4cm. Vypočítejte obvod. Proveďte náčrtek. - Poloměr 10
 Poloměr kružnice r=8,9 cm, tětiva AB této kružnice má délku 16 cm. Vypočítej vzdálenost tětivy AB od středu kružnice .
Poloměr kružnice r=8,9 cm, tětiva AB této kružnice má délku 16 cm. Vypočítej vzdálenost tětivy AB od středu kružnice . - Kružnice
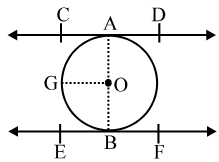
 Kružnice s průměrem 17cm, horní tětivou |CD|=10,2cm a dolní tětivou |EF|=7,5cm, kde pro středy tetiv H, G platí |EH|=1/2 |EF| a |CG|=1/2 |CD|, určete vzdálenost mezi bodem G a H. CD II EF.
Kružnice s průměrem 17cm, horní tětivou |CD|=10,2cm a dolní tětivou |EF|=7,5cm, kde pro středy tetiv H, G platí |EH|=1/2 |EF| a |CG|=1/2 |CD|, určete vzdálenost mezi bodem G a H. CD II EF.
