Vnější dotyk
Sestrojte kružnice k1 ( S1; 1,5 cm), k2 ( S2 ; 2 cm) a k3 ( S3 ; 2,5 cm ), tak aby měly vždy dvě vnější dotyk. Vypočtěte obvod trojúhelníka S1S2S3.
Správná odpověď:
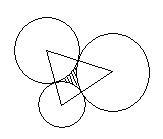
Tipy na související online kalkulačky
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
planimetrietémaÚroveň náročnosti úkolu
Související a podobné příklady:
- Kruh-výseč
Rovnostrannému trojúhelníku o straně 17 je vepsána kruhová výseč, jejíž střed je v jednom z vrcholů trojúhelníku a oblouk se dotýká protější strany. Vypočtěte: a) délku oblouku výseče b) poměr obvodu výseče v ku obvodu trojúhelníka - Kružnice s dvěma tětivami
Dány jsou dvě úsečky různých délek. Sestrojte kružnici k tak, aby obě úsečky byly jejími tětivami. - Smíšená čísla
Přepište smíšená čísla tak, aby zlomky měly stejný jmenovatel: 5 1/5 - 2 2/3 - Je dán 14
Je dán trojúhelník ABC a kružnice vepsaná do tohoto trojúhelníka o poloměru 15. Bod T je bodem dotyku vepsané kružnice se stranou BC. Jaká je plocha trojúhelníka ABC jestliže |BT| = 25 a |TC| = 26? - Dvě tečny
Na obrázku je kružnice k se středem S a poloměrem 5 cm a bod A, který je od středu S vzdálen 13 cm. Z bodu A jsou ke kružnici k sestrojené dvě tečny p, q s body dotyku P, Q. Kromě toho je ke kružnici k sestrojená další tečna t, který protíná tečny p, q v - Povrch potrubí
Vypočítej povrch části potrubí, pokud: vnější průměr = 40 cm; délka = 3 m - Kovová trubka
Vypočtěte hmotnost kovové trubky 8 dm dlouhé, když vnější poloměr je 5 cm a vnitřní poloměr je 4,5 cm a 1 cm³ tohoto kovu má hmotnost 9,5 g.
