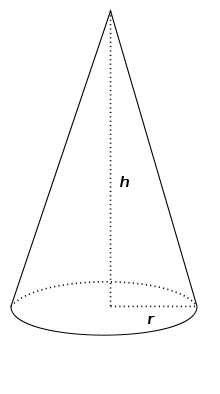
Rotační kužel 6
V rotačního kuželu = 100π
S rotačního kuželu = 90π
v=?
r=?
Vaše odpověď:
S rotačního kuželu = 90π
v=?
r=?
Vaše odpověď:
Tipy na související online kalkulačky
Hledáte pomoc s výpočtem kořenů kvadratické rovnice?
Máte soustavu rovnic a hledáte kalkulačku soustavy lineárních rovnic?
Tip: Převody jednotky objemu vám pomůže naše kalkulačka pro převody jednotek objemu.
Máte soustavu rovnic a hledáte kalkulačku soustavy lineárních rovnic?
Tip: Převody jednotky objemu vám pomůže naše kalkulačka pro převody jednotek objemu.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
algebraaritmetikastereometrieplanimetrieJednotky fyzikálních veličinÚroveň náročnosti úkolu
Související a podobné příklady:
- Kužel - rs
Vypočtěte objem rotačního kuželu o poloměru podstavy 26,3 cm a straně 38,4 cm. - Střecha
Střecha má tvar pláště rotačního kuželu s průměrem podstavy 6 m a výškou 2,5 m. Kolik korun bude stát plech na pokrytí střechy, jestliže 1 m² plechu stojí 152 Kč a jestliže na spoje, překrytí a odpad je nutné zakoupit 15% navíc? - Spotřeba papíru na stínítko
Stínítko lampy má tvar pláště rotačního kuželu se stranou 32 cm a průměrem podstavy 46 cm. Vypočítejte spotřebu papíru na jeho výrobu pokud předpokládáte, že odpad bude 6% - Povrch a objem
Vypočítejte povrch a objem rotačního kužele, jestliže jeho strana je dlouhá 150 mm a obvod podstavy je 43,96 cm. - Určení x z procent
Urči x, pokud 98% z x se rovná 196. - Rovnice
Najděte X v této jednoduché rovnici: X/9 = 96/108 - Rovnice s dvěma poměry
Riešte rovnice s dvěma poměry: x:14=28:196
