Druhá odmocnina
Pokud je druhá odmocnina z 3m2 +22 -x = 0 a x = 7, což je m?
Správná odpověď:
Tipy na související online kalkulačky
Hledáte pomoc s výpočtem kořenů kvadratické rovnice?
Máte lineární rovnici nebo soustavu rovnic a hledáte její řešení? Nebo máte kvadratickou rovnici?
Máte lineární rovnici nebo soustavu rovnic a hledáte její řešení? Nebo máte kvadratickou rovnici?
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
Související a podobné příklady:
- Rýze kvadratická rovnice
 Řešte ryze kvadratickou rovnici -5x² +7 = 0.
Řešte ryze kvadratickou rovnici -5x² +7 = 0. - Kvadratická rovnice
 Řešte kvadratickou rovnici: 2x2-76x+722=0
Řešte kvadratickou rovnici: 2x2-76x+722=0 - Hodnota
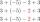 Určete hodnotu výrazu 3a + 2b - a² - 4b² pro hodnoty proměnných : a) a = - 1, b = 3 b) a = 2, b = -1 c) a = -2, b = -3 d) a = 4, b = 2 e) a = -5, b = 0
Určete hodnotu výrazu 3a + 2b - a² - 4b² pro hodnoty proměnných : a) a = - 1, b = 3 b) a = 2, b = -1 c) a = -2, b = -3 d) a = 4, b = 2 e) a = -5, b = 0 - Kvadr. rovnica
 Rešte kvadratickou rovnici: 2x²- 2(x-7)²+5x=0
Rešte kvadratickou rovnici: 2x²- 2(x-7)²+5x=0
- Kvadratická rovnice
 Kvadratická rovnice -4x²+bx+c=0 má kořeny x1 = 85 a x2 = -46. Vypočítejte koeficienty b a c.
Kvadratická rovnice -4x²+bx+c=0 má kořeny x1 = 85 a x2 = -46. Vypočítejte koeficienty b a c. - Doplnění na čtverec
 Vyřešte kvadratickou rovnici: m² = 4m + 20 pomocí metody doplnění na čtverec nebo doplnění do čtverce.
Vyřešte kvadratickou rovnici: m² = 4m + 20 pomocí metody doplnění na čtverec nebo doplnění do čtverce. - Střed
 Vypočítejte súradnice středu kružnice: x² +14x + y² -4y +52 = 0
Vypočítejte súradnice středu kružnice: x² +14x + y² -4y +52 = 0 - Na přímce 3
 Na přímce p: 2x + y + 1 = 0 najděte bod A ∈ p, který je nejblíže bodu P =(1,0)
Na přímce p: 2x + y + 1 = 0 najděte bod A ∈ p, který je nejblíže bodu P =(1,0) - Věžička
 Věžička má tvar pravidelného čtyřbokého jehlanu s podstavnou hranou délky 0,8 m. Výška věžičky je 1,2 m. Kolik metrů čtverečných je potřeba na její pokrytí, počítáne-li na odpad 10% plechu navíc.
Věžička má tvar pravidelného čtyřbokého jehlanu s podstavnou hranou délky 0,8 m. Výška věžičky je 1,2 m. Kolik metrů čtverečných je potřeba na její pokrytí, počítáne-li na odpad 10% plechu navíc.
- Cifry A,B,C
 Pro různé cifry A,B,C platí: druhá odmocnina ze BC se rovná A a součet B+C se rovná A. Urči A+2B+3C. BC uvažujte ako dvojciferné číslo, nie jako súčin.
Pro různé cifry A,B,C platí: druhá odmocnina ze BC se rovná A a součet B+C se rovná A. Urči A+2B+3C. BC uvažujte ako dvojciferné číslo, nie jako súčin. - 3x^2+bx+c=0 82539
 V rovnici 3x²+bx+c=0 je jeden kořen x1 = -3/2. Určete číslo c tak, aby číslo 4 bylo kořenem rovnice. Nápověda - použijte Vietovy vzorce.
V rovnici 3x²+bx+c=0 je jeden kořen x1 = -3/2. Určete číslo c tak, aby číslo 4 bylo kořenem rovnice. Nápověda - použijte Vietovy vzorce. - Hodnotu 3782
 Určete hodnotu x, pokud x ^ 0,5=6
Určete hodnotu x, pokud x ^ 0,5=6 - Bikvadratická
 Zavedením nové proměnné řešte bikvadratickú rovnici: -2 x 4 +400 x² -1568=0
Zavedením nové proměnné řešte bikvadratickú rovnici: -2 x 4 +400 x² -1568=0 - Vzdálenost 83160
 Vypočítej vzdálenost bodu A[ 4; 2; -3 ] od roviny : 2x - 2y + z + 5 = 0
Vypočítej vzdálenost bodu A[ 4; 2; -3 ] od roviny : 2x - 2y + z + 5 = 0
- Kradnú politici
 X + Y = 31835 X je množství, které nakradli 1,2 a 3 Y je množství, které nakradli 4 a 5 1. ukradl polovinu X, 2 . polovinu zbytku a ještě 3 k tomu 3. ukradl 6801,5 4. Ukradl 1/9 z Y, což je 513 5. Nakradl zbytek
X + Y = 31835 X je množství, které nakradli 1,2 a 3 Y je množství, které nakradli 4 a 5 1. ukradl polovinu X, 2 . polovinu zbytku a ještě 3 k tomu 3. ukradl 6801,5 4. Ukradl 1/9 z Y, což je 513 5. Nakradl zbytek - Určete 47
 Určete rovnici kružnice, která prochází bodem M(-1,2) a N( 3,0) a jejíž střed leží na přímce p: x=-3+t, y=-1+t,
Určete rovnici kružnice, která prochází bodem M(-1,2) a N( 3,0) a jejíž střed leží na přímce p: x=-3+t, y=-1+t, - Rovnice o dvou neznámých
 Rěšte soustavu: 15x+30y=-20 0,3x-0,2y=0,4
Rěšte soustavu: 15x+30y=-20 0,3x-0,2y=0,4
