Goniometrie a trigonometrie - slovní úlohy a příklady - strana 21 z 32
Počet nalezených příkladů: 627
- Vzducholoď
 Vzducholoď je ve výšce x nad zemí. Pavel ji sleduje z místa A pod výškovým úhlem 18 stupnu 26 minut. V tutéž chvíli ji vidí Petr z malého letadla, které zrovna prolétá nad Pavlem ve výšce 150m. Petr vidí vzducholoď pod výškovým úhlem 11 stupnu a 46 minut.
Vzducholoď je ve výšce x nad zemí. Pavel ji sleduje z místa A pod výškovým úhlem 18 stupnu 26 minut. V tutéž chvíli ji vidí Petr z malého letadla, které zrovna prolétá nad Pavlem ve výšce 150m. Petr vidí vzducholoď pod výškovým úhlem 11 stupnu a 46 minut. - Pravidelný 8
 Pravidelný čtyřboký jehlan má podstavnou hranu a=1,56 dm a výšku v= 2,05dm. Vypočtěte : a) odchylku roviny boční stěny od roviny podstavy b) odchylku boční hrany od roviny podstavy
Pravidelný čtyřboký jehlan má podstavnou hranu a=1,56 dm a výšku v= 2,05dm. Vypočtěte : a) odchylku roviny boční stěny od roviny podstavy b) odchylku boční hrany od roviny podstavy - Cena střechy
 Přístřešek na auto je třeba přikrýt valbovou střechou s obdélníkovým průřezem 8 m x 5 m. Všechny střešní plochy mají stejný sklon 30°. Určete cenu a hmotnost střechy, pokud 1 m² stojí 270 € a váží 43 kg.
Přístřešek na auto je třeba přikrýt valbovou střechou s obdélníkovým průřezem 8 m x 5 m. Všechny střešní plochy mají stejný sklon 30°. Určete cenu a hmotnost střechy, pokud 1 m² stojí 270 € a váží 43 kg. - Rovnoramenný
 Rovnoramenný lichoběžník ABCD má základny 18 cm a 12 cm. Úhel u vrcholu A má velikost 60°. Jaký je obvod a obsah lichoběžníku?
Rovnoramenný lichoběžník ABCD má základny 18 cm a 12 cm. Úhel u vrcholu A má velikost 60°. Jaký je obvod a obsah lichoběžníku? - Na vrcholu
 Na vrcholu hory stojí hrad, který má věž vysokou 30m. Křižovatku cest v údolí vidíme z vrcholu věže a od její paty v hloubkových úhlech 32° 50 'a 30° 10'. Jak vysoko je vrchol hory nad křižovatkou?
Na vrcholu hory stojí hrad, který má věž vysokou 30m. Křižovatku cest v údolí vidíme z vrcholu věže a od její paty v hloubkových úhlech 32° 50 'a 30° 10'. Jak vysoko je vrchol hory nad křižovatkou? - Trojboký hranol
 Rovina, která prochází hranou AB a středem hrany CC' pravidelného trojbokého hranolu ABCA'B'C', svírá s podstavou úhel 46 stupňů, |AB| = 12 cm. Vypočítejte objem hranolu.
Rovina, která prochází hranou AB a středem hrany CC' pravidelného trojbokého hranolu ABCA'B'C', svírá s podstavou úhel 46 stupňů, |AB| = 12 cm. Vypočítejte objem hranolu. - Sklon tratě
 Vypočítejte průměrný sklon tratě (v promile a také ve stupních) z Prievidze (309 mnm) do stanice Bratislava (152 mnm), pokud trať je dlouhá 158 km.
Vypočítejte průměrný sklon tratě (v promile a také ve stupních) z Prievidze (309 mnm) do stanice Bratislava (152 mnm), pokud trať je dlouhá 158 km. - Kvádr
 Vypočítejte objem kvádru ABCDEFGH, jestliže |AB| = 20 cm, |BC| = 8 cm a úhel ∠CDG = 60,6°
Vypočítejte objem kvádru ABCDEFGH, jestliže |AB| = 20 cm, |BC| = 8 cm a úhel ∠CDG = 60,6° - Vypočtěte 10
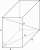 Vypočtěte velikost odchylky tělesové úhlopřičky a boční hrany c kvádru o rozměrech: a=28cm, b=45cm a c=73cm. Dále vypočtěte velikost odchylky tělesové úhlopřičky od roviny podstavy.
Vypočtěte velikost odchylky tělesové úhlopřičky a boční hrany c kvádru o rozměrech: a=28cm, b=45cm a c=73cm. Dále vypočtěte velikost odchylky tělesové úhlopřičky od roviny podstavy. - Silnice - stoupání
 Na dopravní značce, která informuje o stoupání silnice, je údaj 6,7 %. Určete úhel stoupání cesty. Jaký výškový rozdíl překonalo auto, které ujelo po této cestě 2,8 km?
Na dopravní značce, která informuje o stoupání silnice, je údaj 6,7 %. Určete úhel stoupání cesty. Jaký výškový rozdíl překonalo auto, které ujelo po této cestě 2,8 km? - V terénu - věta SSU
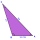 V terénu byla měřena vzdálenost bodů P a Q rovná 356 m. Úsečka PQ je vidět od pozorovatele pod zorným úhlem 107°22'. Vzdálenost pozorovatele od místa P je 271 m. Urči zorný úhel, pod kterým je vidět místo P a pozorovatele.
V terénu byla měřena vzdálenost bodů P a Q rovná 356 m. Úsečka PQ je vidět od pozorovatele pod zorným úhlem 107°22'. Vzdálenost pozorovatele od místa P je 271 m. Urči zorný úhel, pod kterým je vidět místo P a pozorovatele. - Urči povrch
 Urči povrch kužele výšky 30 cm, jehož strana svírá s rovinou podstavy úhel 60°.
Urči povrch kužele výšky 30 cm, jehož strana svírá s rovinou podstavy úhel 60°. - Odchylka přímek 2
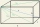 Určite odchylku přímek AH, BH v kvádru ABCDEFGH, je-li dáno |AB| = 3cm, |AD| = 2cm, |AE| = 4cm
Určite odchylku přímek AH, BH v kvádru ABCDEFGH, je-li dáno |AB| = 3cm, |AD| = 2cm, |AE| = 4cm - Divnej kužel
 Rotační kužel má výšku 72cm a úhel při vrcholu 72°. Určete objem koule se stejným poloměrem jako kužel.
Rotační kužel má výšku 72cm a úhel při vrcholu 72°. Určete objem koule se stejným poloměrem jako kužel. - Určete
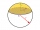 Určete objem kulového odseku, pokud poloměr jeho podstavy je 10 cm a velikost středového úhlu ω = 120 stupňů.
Určete objem kulového odseku, pokud poloměr jeho podstavy je 10 cm a velikost středového úhlu ω = 120 stupňů. - Osmiboký jehlan
 Urči objem pravidelného osmibokého jehlanu, jehož výška v = 100 a úhel boční hrany s rovinou podstavy je α = 60°.
Urči objem pravidelného osmibokého jehlanu, jehož výška v = 100 a úhel boční hrany s rovinou podstavy je α = 60°. - Rovnoběžka
 Vypočítejte délku rovnoběžky 48 stupňů a 10 minut.
Vypočítejte délku rovnoběžky 48 stupňů a 10 minut. - Komín 5
 Jak vysoký je komín teplárny, stojí-li pozorovatel od paty komínu 26 m a vidí-li vrchol komínu pod úhlem 67°.
Jak vysoký je komín teplárny, stojí-li pozorovatel od paty komínu 26 m a vidí-li vrchol komínu pod úhlem 67°. - Vypočítejte
 Vypočítejte délku tětivy v kružnici o poloměru 25 cm, které přísluší obvodový úhel 26°.
Vypočítejte délku tětivy v kružnici o poloměru 25 cm, které přísluší obvodový úhel 26°. - V trojúhelníku 8
 V trojúhelníku ABC znáte poměr délek stran a:b:c=3:4:6. Vypočítejte velikosti úhlů trojúhelníku ABC.
V trojúhelníku ABC znáte poměr délek stran a:b:c=3:4:6. Vypočítejte velikosti úhlů trojúhelníku ABC.
Máš příklad z matematiky, který jsi tady nenašel vyřešený? Pošli nám příklad a my Ti ho zkusíme vypočítat.
