Kombinatorika - slovní úlohy a příklady - strana 19 z 53
Počet nalezených příkladů: 1056
- Klávesy
 Míša mel na poličce malé klávesy, které vidíte na obrázku. Na bílých klávesách byly vyznačeny jejich tóny. Klávesy našla malá Klára. Když je brala z poličky, vypadly jí z ruky a všechny bílé klávesy se z nich vysypaly. Aby se bratr nezlobil, začala je Klá
Míša mel na poličce malé klávesy, které vidíte na obrázku. Na bílých klávesách byly vyznačeny jejich tóny. Klávesy našla malá Klára. Když je brala z poličky, vypadly jí z ruky a všechny bílé klávesy se z nich vysypaly. Aby se bratr nezlobil, začala je Klá - Pravděpodobnost pořadí
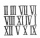 Skupina n lidí, mezi kterými jsou Jano a Fero se náhodně seřadí do zástupu. Jaká je pravděpodobnost, že mezi Janem a Ferem bude právě r lidí (r < n-2)?
Skupina n lidí, mezi kterými jsou Jano a Fero se náhodně seřadí do zástupu. Jaká je pravděpodobnost, že mezi Janem a Ferem bude právě r lidí (r < n-2)? - Kniha
 Kniha má 88 stran. Kolikrát je při číslovaný knížky použita číslice 4?
Kniha má 88 stran. Kolikrát je při číslovaný knížky použita číslice 4? - Skupina
 Skupina 10 děvčat se má rozdělit na dvě skupiny tak, aby v každé byli nejméně 4 děvčata. Kolika způsoby to lze provést?
Skupina 10 děvčat se má rozdělit na dvě skupiny tak, aby v každé byli nejméně 4 děvčata. Kolika způsoby to lze provést? - Manažer kvality
 Představte si, že jste manažerem kvality na výrobní lince montující elektrospotřebiče. Do spotřebičů se montují tištěné stroje, na jejich bezvadnosti závisí funkčnost výrobku. Linka je vybavena testerem-kontrolní zařízením, které s pravděpodobností 0,999
Představte si, že jste manažerem kvality na výrobní lince montující elektrospotřebiče. Do spotřebičů se montují tištěné stroje, na jejich bezvadnosti závisí funkčnost výrobku. Linka je vybavena testerem-kontrolní zařízením, které s pravděpodobností 0,999 - Zahradník 6
 Zahradník má osázet tři záhony, každý právě jedním druhem rostlin. Možností, jak osázet tyto 3 záhony třemi různými druhy rostlin, je o 133 méně než možností, jak lze tyto záhony osázet nejvýše třemi různými druhy rostlin. Počet rostlin každého druhu by p
Zahradník má osázet tři záhony, každý právě jedním druhem rostlin. Možností, jak osázet tyto 3 záhony třemi různými druhy rostlin, je o 133 méně než možností, jak lze tyto záhony osázet nejvýše třemi různými druhy rostlin. Počet rostlin každého druhu by p - Výběr brýlí
 Miloš pracuje v optice. Kamarádovi Martinovi pomáhá při výběru skel do dioptrických brýlí. Ty mohou mít: - speciální úpravu proti poškrábání, - antireflex – zajišťuje větší propustnost světla do oka, - heliovar – ztmavnutí skel při pobytu na denním světle
Miloš pracuje v optice. Kamarádovi Martinovi pomáhá při výběru skel do dioptrických brýlí. Ty mohou mít: - speciální úpravu proti poškrábání, - antireflex – zajišťuje větší propustnost světla do oka, - heliovar – ztmavnutí skel při pobytu na denním světle - Sedemsegmentovka
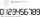 Lenka se bavila tím, že vyťukávala na kalkulačce (sedmisegmentový display) čísla, přičemž používala pouze číslice od 2 do 9. Zápisy některých čísel měly tu vlastnost, že jejich obraz v osové nebo středové souměrnosti byl opět zápisem nějakého čísla. Určet
Lenka se bavila tím, že vyťukávala na kalkulačce (sedmisegmentový display) čísla, přičemž používala pouze číslice od 2 do 9. Zápisy některých čísel měly tu vlastnost, že jejich obraz v osové nebo středové souměrnosti byl opět zápisem nějakého čísla. Určet - Roberti (Z7–I–4)
 V robotí škole do jedné třídy chodí dvacet robotů Robertů, kteří jsou očíslováni Robert 1 až Robert 20. Ve třídě je zrovna napjatá atmosféra, mluví spolu jen někteří roboti. Roboti s lichým číslem nemluví s roboty se sudým číslem. Mezi Roberty s lichým čí
V robotí škole do jedné třídy chodí dvacet robotů Robertů, kteří jsou očíslováni Robert 1 až Robert 20. Ve třídě je zrovna napjatá atmosféra, mluví spolu jen někteří roboti. Roboti s lichým číslem nemluví s roboty se sudým číslem. Mezi Roberty s lichým čí - Pravděpodobnost nekvalitního kabátu
 Oděvní firma vyrábí tři druhy kabátů. Týdenní produkce je 400 prvního typu, 370 druhého a 230 třetího typu. Dlouhodobým pozorováním se zjistilo, že kvalitních kabátů je z prvního typu 2/3, druhého typu 7/9 a třetího typu 4/5. Jaká je pravděpodobnost, že a
Oděvní firma vyrábí tři druhy kabátů. Týdenní produkce je 400 prvního typu, 370 druhého a 230 třetího typu. Dlouhodobým pozorováním se zjistilo, že kvalitních kabátů je z prvního typu 2/3, druhého typu 7/9 a třetího typu 4/5. Jaká je pravděpodobnost, že a - Taneční páry
 Do taneční přišlo 32 chlapců a 34 dívek. Kolik různých tanečních párů mohou vytvořit za předpokladu, že pro každý pár je zadáno: může tančit jen 1 min, poté se musí vystřídat za 5 s. Vypočítejte, jak dlouho by musel trvat taneční večer, aby se vystřídali
Do taneční přišlo 32 chlapců a 34 dívek. Kolik různých tanečních párů mohou vytvořit za předpokladu, že pro každý pár je zadáno: může tančit jen 1 min, poté se musí vystřídat za 5 s. Vypočítejte, jak dlouho by musel trvat taneční večer, aby se vystřídali - Fixy v penálu
 V ostatních dnech mám často před očima hlavně dvě barvy – modrou a žlutou. Je mi smutno z toho, co se děje. Proto i dnes mám pro vás roli o barvách. V penálu mám 5 fixů: modrou, žlutou, zelenou, červenou a fialovou. Kolik mám možností jich v penálu uložit
V ostatních dnech mám často před očima hlavně dvě barvy – modrou a žlutou. Je mi smutno z toho, co se děje. Proto i dnes mám pro vás roli o barvách. V penálu mám 5 fixů: modrou, žlutou, zelenou, červenou a fialovou. Kolik mám možností jich v penálu uložit - Tombola
 Kolik tombolových lístků si musí koupit Peter v tombole s vydanými 200 lístky, pokud chce mít jistotu, že vyhraje alespoň 3 ceny? V tombole se losuje 30 cen.
Kolik tombolových lístků si musí koupit Peter v tombole s vydanými 200 lístky, pokud chce mít jistotu, že vyhraje alespoň 3 ceny? V tombole se losuje 30 cen. - Svetry
 Mám vedle sebe umístit 4 svetry, dva jsou bílé, 1 červenej a 1 zelený. Kolika způsoby to jde?
Mám vedle sebe umístit 4 svetry, dva jsou bílé, 1 červenej a 1 zelený. Kolika způsoby to jde? - Dva doktoři
 Lékař A určí správnou diagnózu s pravděpodobností 87% a lékař B s pravděpodobností 76%. Vypočítejte s jakou pravděpodobností pacient je si jistý diagnózou pokud jde na vyšetření k oběma lékařům.
Lékař A určí správnou diagnózu s pravděpodobností 87% a lékař B s pravděpodobností 76%. Vypočítejte s jakou pravděpodobností pacient je si jistý diagnózou pokud jde na vyšetření k oběma lékařům. - Kombinatorické úlohy
 1. Ve třídě máte 15 žáků. Kolika způsoby můžeme vybrat čtyři k vyzkoušení? 2. Kolika způsoby můžeme vybrat ze sedmových karet (32 karet) libovolné dvě karty? 3. Kolika způsoby můžeme rozdělit 12 žáků na dvě šestičlenná družstva? .4. Kolika způsoby může uč
1. Ve třídě máte 15 žáků. Kolika způsoby můžeme vybrat čtyři k vyzkoušení? 2. Kolika způsoby můžeme vybrat ze sedmových karet (32 karet) libovolné dvě karty? 3. Kolika způsoby můžeme rozdělit 12 žáků na dvě šestičlenná družstva? .4. Kolika způsoby může uč - Permutace a kombinace
 Kolika různými způsoby můžeme usadit tři lidi na tři židle, čtyři na čtyři, pěti na pět a šesti na šest židlí? Najděte společné vlastnosti při výběru objektů z hlediska kombinatoriky. Zjistěte princip výpočtu všech možností splňujících podmínky v zadání ú
Kolika různými způsoby můžeme usadit tři lidi na tři židle, čtyři na čtyři, pěti na pět a šesti na šest židlí? Najděte společné vlastnosti při výběru objektů z hlediska kombinatoriky. Zjistěte princip výpočtu všech možností splňujících podmínky v zadání ú - Vagonky
 Máme šest vagonků dva bíle, dva modré a dva červené. Sestavujeme z nich vlaky, vagonky stejné barvy jsou úplně stejné, takže když ve vlaku přehodíme jenom dva bílé vagonky, tak je to pořád stejný vlak, protože nepoznám žádný rozdíl. Kolik různých vlaků mů
Máme šest vagonků dva bíle, dva modré a dva červené. Sestavujeme z nich vlaky, vagonky stejné barvy jsou úplně stejné, takže když ve vlaku přehodíme jenom dva bílé vagonky, tak je to pořád stejný vlak, protože nepoznám žádný rozdíl. Kolik různých vlaků mů - Pravděpodobnost správných odpovědí
 Studenti píší kroužkovací test s 10 otázkami, s možnostmi odpovědí a), b), c), přičemž je vždy správná pouze jedna odpověď. Učitel jim řekl, že v testu je počet správných odpovědí následující: možnost a) 5krát, možnost b) 3krát, možnost c) 2krát. Jaká je
Studenti píší kroužkovací test s 10 otázkami, s možnostmi odpovědí a), b), c), přičemž je vždy správná pouze jedna odpověď. Učitel jim řekl, že v testu je počet správných odpovědí následující: možnost a) 5krát, možnost b) 3krát, možnost c) 2krát. Jaká je - Turnaj ve vybíjené
 Na turnaj ve vybíjené se přihlásilo 8 týmů, z nichž se losem vytvořily dvojice. V prvním kole každá dvojice odehrála jeden zápas. Vítězové odehráli semifinálové zápasy a vítězové semifinále odehráli poslední, finálový zápas, který určil celkového vítěze t
Na turnaj ve vybíjené se přihlásilo 8 týmů, z nichž se losem vytvořily dvojice. V prvním kole každá dvojice odehrála jeden zápas. Vítězové odehráli semifinálové zápasy a vítězové semifinále odehráli poslední, finálový zápas, který určil celkového vítěze t
Máš příklad z matematiky, který jsi tady nenašel vyřešený? Pošli nám příklad a my Ti ho zkusíme vypočítat.
