Příklady na kužel - strana 3 z 14
Počet nalezených příkladů: 263
- Kolik
Kolik m² měděného plechu třeba na výměnu střechy věže kuželovitého tvaru, jejíž průměr je 13 metrů a výška 24 metrů, pokud na zahnutí a odpad počítáme 8% materiálu? - Rovnostranné těleso
Rotační těleso vzniklo rotací rovnostranného trojúhelníku o délce strany a=2 cm kolem jedné z jeho stran. Vypočítejte objem tohoto rotačního tělesa. - Šikmo
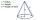Obrázek znázorňuje kužel se šikmou výškou (stranou) 10,5 cm. Zakřivená plocha kužele 115,5 cm². Vypočtěte na 3 platné číslice: * Poloměr základny * výšku * Objem kužele - Spotřeba papíru na stínítko
Stínítko lampy má tvar pláště rotačního kuželu se stranou 32 cm a průměrem podstavy 46 cm. Vypočítejte spotřebu papíru na jeho výrobu pokud předpokládáte, že odpad bude 6% - Průměr
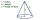Průměr základny pravoúhlého kužele je 16 cm a jeho šikmá výška je 12 cm. A. ) Zjistěte kolmou výšku kužele na 1 desetinné místo. B. ) Najděte objem kužele a přepočítejte ho na 3 významné číslo. Použijte pi = 3,14 - Správce hradu
Správce hradu se pokouší odhadnout, kolik čtverečných metrů plechu bude přibližně třeba na novou střechu věže. Střecha má tvar kužele. Správce hradu ví, že průměr věže je 4,6 metru a výška je 5,2 metru. Kolik čtverečných metrů střecha měří? - Rotační kužel
Objem rotačního kužele je 733 cm³ a strana kužele svírá s rovinou podstavy úhel 75°. Vypočítejte obsah pláště rotačního kužele. - Kužel
Rotační kužel o výšce 19 cm a objemu 2148 cm³ je ve třetině výšky (měřeno zespoda) rozříznut rovinou rovnoběžnou s podstavou. Určete poloměr a obvod kruhovéh řezu. - Spotřeba plechu
Střecha věže má tvar pláště rotačního kužele o průměru podstavy 4,3m. Odchylka strany od roviny podstavy je 36°. Vypočítejte spotřebu plechu na pokrytí střechy, počítáme-li 8 % na odpad. - Osový řez
Osový řez kužele je rovnoramenný trojúhelník, v němž je poměr průměru kužele a stěny kužele 2:3. Vypočtěte jeho objem, pokud víte, že jeho plocha je 314 cm čtverečních. - Kužel
Vypočtěte objem a plochu kužele, jehož výška je 10 cm a v osovém řezu svírá se stěnou kužele úhel 30 stupňů. - Zakrytí hromady soli
Hromada soli byla uložena ve tvaru kužele. Pan Terwilliker ví, že hromada je 20 stop vysoká a 102 stop v obvodu na základně. Jaká plocha kónické plachty (velký kus materiálu) je potřebná k zakrytí hromady? - Stínítko na lampe
Stínidlo na lampu na tvář seříznutého kužele o výšce 20 cm. Horní průměr stínítka je 13 cm, dolní 36 cm a strana svírá s dolním průměrem úhel 60 stupňů. Nejméně kolik látky je potřeba k výrobě tohoto stínítka? - Stínidlo
Stínidlo ve tvaru kužele má průměr 30 cm a výšku 10 cm. Kolik cm² materiálu budeme potřebovat, počítáme-li 10% na odpad? - Kužel 16
Povrch rotačního kužele je 30 cm2, obsah jeho pláště je 20 cm². Vypočtěte odchylku strany tohoto kužele od roviny podstavy. - Kužel - RS trojúhelník
Povrch kužele je 388,84 cm², osový řez je rovnostranný trojúhelník. Určete objem kužele. - Čepice
Šaškova čepice má tvar rotačního kužele. Vypočítejte kolik papíru je třeba utratit na čepici 50 cm vysokou na obvod hlavy 60 cm. - Objem kužele Vypočítejte objem kužele, který vznikne rotací rovnoramenného trojúhelníku kolem výšky na základnu, pokud trojúhelník má rameno dlouhé 15 cm a výšku na základnu 12 cm. Při výpočtu použijte hodnotu pi = 3,14 a výsledek zaokrouhlete na jedno desetinné místo
- Urči poloměr
Urči poloměr podstavy kužele, jestliže jeho plášť se rozvine v kruhovou výseč s poloměrem „s"=10 a středovým úhlem x=60°. r=?, o=? - Povrch kužele
Vypočítejte povrch a objem rotačního kužele, jehož podstava má průměr 6cm, a jeho výška 4cm.
Máš příklad z matematiky, který jsi tady nenašel vyřešený? Pošli nám příklad a my Ti ho zkusíme vypočítat.
