Šikmo

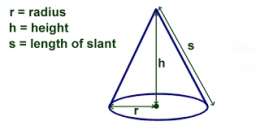
Obrázek znázorňuje kužel se šikmou výškou (stranou) 10,5 cm. Zakřivená plocha kužele 115,5 cm². Vypočtěte na 3 platné číslice:

* Poloměr základny
* výšku
* Objem kužele

Vaše odpověď:

Pomozte nám příklad zlepšit. Pokud jste našli chybu, dejte nám vědět. Děkujeme!

Tipy na související online kalkulačky

Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Tip: Převody jednotky objemu vám pomůže naše kalkulačka pro převody jednotek objemu.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.

K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:

algebra

úpravy výrazů

aritmetika

odmocnina

stereometrie

kužel

planimetrie

Pythagorova věta
pravoúhlý trojúhelník
kruh, kružnice
obsah
trojúhelník

Jednotky fyzikálních veličin

objem

Úroveň náročnosti úkolu

9. ročník
střední škola

Doporučujeme k tomuto príkladu si prohlédnout toto výukové video: video1

Související a podobné příklady:

Šikma strana
Kužel má šikmou stranu délky 10 cm a zakřivenou plochu pláště 50 pí čtverečních cm. Najděte poloměr základny kužele.
Poloměr podstavy
Jak se změní objem rotačního kužele, pokud: a) zdvojnásobíme poloměr podstavy b) 3 krát zmenšíme výšku c) 5 krát zmenšíme poloměr podstavy
Seříznutý kužel
Vypočítejte objem komolého kužele s poloměry podstáv r₁=19 cm, r₂ = 6 cm a výškou v = 22 cm.
Objem kužele
Vypočítejte objem kužele s poloměrem podstavy r a výškou v. a) r = 6 cm, v = 8 cm b) r = 0,9 m, v = 2,3 m c) r = 1,4 dm, v = 30 dm
Komolý kužel
Vypočtěte výšku rotačního komolého kužele, je-li dán jeho objem V=1008 cm³ a poloměry podstav r₁=7 cm a r₂=7,3 cm.
Řezy kužele
Kužel s poloměrem podstavy 16 cm a výškou 16 cm rozdělíme rovinami rovnoběžnými s podstavou na tři tělesa. Roviny rozdělí výšku kužele na tři stejné části. Určete poměr objemů největšího a nejmenšího vzniklého tělesa.
Šikmá výška
Šikmá výška kužele je 5 cm a poloměr jeho základny je 3 cm. Najděte objem kužele.