Šikmina
Obrázok znázorňuje kužeľ so šikmou výškou (stranou) 10,5 cm. Zakrivená plocha kužeľa 115,5 cm2. Vypočítajte na 3 platné číslice:
* polomer základne
* výšku
* objem kužeľa
* polomer základne
* výšku
* objem kužeľa
Správna odpoveď:
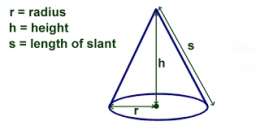
Tipy na súvisiace online kalkulačky
Tip: premeniť jednotky objemu vám pomôže naša kalkulačka premeny jednotiek objemu.
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
- algebra
- vyjadrenie neznámej zo vzorca
- stereometria
- kúžeľ
- planimetria
- Pytagorova veta
- pravouhlý trojuholník
- kruh, kružnica
- trojuholník
Jednotky fyzikálnych veličín:
Úroveň náročnosti úlohy:
Súvisiace a podobné príklady:
- Zmena objemu
Ako sa zmení objem rotačného kužeľa, ak: a) zdvojnásobíme polomer podstavy b) 3 krát zmenšíme výšku c) 5 krát zmenšíme polomer podstavy - Tienidlo 3
Tienidlo lampy má tvar plášťa rotačného kužela so stranou 32 cm a priemerom podstavy 46 cm. Vypočítajte spotrebu papiera na jeho výrobu ak predpokladáte, že odpad bude 6% - Rezy kužela
Kužeľ s polomerom podstavy 16 cm a výškou 11 cm rozdelíme rovinami rovnobežnými s podstavou na tri telesá. Roviny rozdelia výšku kužeľa na tri rovnaké časti. Určte pomer objemov najväčšieho a najmenšieho vzniknutého telesa. - Objem kužeľa
Vypočítajte objem kužeľa s polomerom podstavy r a výškou v. a) r = 6 cm, v = 8 cm b) r = 0,9 m, v = 2,3 m c) r = 1,4 dm, v = 30 dm
- Zrezaný kúžeľ
Vypočítajte objem zrezaného kúžeľa s polomermi podstáv r1=17 cm, r2 = 6 cm a výškou v = 20 cm. - Rotačný kužeľ
Rotačný kužeľ, ktorého výška je rovná obvodu podstavy, má objem 3867 cm³. Vypočítajte polomer podstavnej kružnice a výšku kužeľa. - Rotačný kúžeľ
Vypočítajte objem rotačného kužeľa s polomerom podstavy r=15 cm a výškou v=17 cm.
