Příklady na obsah trojúhelníka - strana 26 z 45
Počet nalezených příkladů: 882
- Pravoúhlý lichoběžník 6
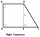 Pravoúhlý lichoběžník ABCD se základnami AB a CD je rozdělen úhlopříčkou AC na dva rovnoramenné pravoúhlé trojúhelníky. Délka úhlopříčky AC je rovna 62 cm. Vypočítejte v cm čtverečných obsah lichoběžníku a vypočítej, o kolik cm se liší obvody trojúhelníků
Pravoúhlý lichoběžník ABCD se základnami AB a CD je rozdělen úhlopříčkou AC na dva rovnoramenné pravoúhlé trojúhelníky. Délka úhlopříčky AC je rovna 62 cm. Vypočítejte v cm čtverečných obsah lichoběžníku a vypočítej, o kolik cm se liší obvody trojúhelníků - Erb
 Třída si vytvořila vlastní erb, který měl tvar složený z rovnoramenného lichoběžníku ABCD (kratší základna je dlouhá a=4,5 cm, delší 2a=9 cm, výška lichoběžníku 6 cm) a půlkruhu se středem S a průměrem AB. Lichoběžník tvořily tři shodné rovnoramenné trojú
Třída si vytvořila vlastní erb, který měl tvar složený z rovnoramenného lichoběžníku ABCD (kratší základna je dlouhá a=4,5 cm, delší 2a=9 cm, výška lichoběžníku 6 cm) a půlkruhu se středem S a průměrem AB. Lichoběžník tvořily tři shodné rovnoramenné trojú - V pravoúhlém 8
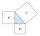 V pravoúhlém trojúhelníku ABC (AB je přepona) platí a : b = 24 : 7 a výška na stranu c = 12,6 cm. Vypočítejte délky stran trojúhelníku ABC.
V pravoúhlém trojúhelníku ABC (AB je přepona) platí a : b = 24 : 7 a výška na stranu c = 12,6 cm. Vypočítejte délky stran trojúhelníku ABC. - Rovnoramenný lichoběžník
 Vypočítejte délku ramen a obsah rovnoramenného lichoběžníku, pokud znáte následující parametry: o = 20 cm (obvod) a = 10 cm, c = 4 cm (délky základen) v = 2 cm (výška)
Vypočítejte délku ramen a obsah rovnoramenného lichoběžníku, pokud znáte následující parametry: o = 20 cm (obvod) a = 10 cm, c = 4 cm (délky základen) v = 2 cm (výška) - Obrazec
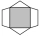 Obrazec se skládá z tmavého čtverce, dvou shodných bílých rovnoramenných trojúhelníků a dvou shodných bílých lichoběžníků. (S každou stranou čtverce splývá základna jednoho bílého útvaru. ) Tmavý čtverec má stranu délky 12 cm a jeho obsah je polovinou obs
Obrazec se skládá z tmavého čtverce, dvou shodných bílých rovnoramenných trojúhelníků a dvou shodných bílých lichoběžníků. (S každou stranou čtverce splývá základna jednoho bílého útvaru. ) Tmavý čtverec má stranu délky 12 cm a jeho obsah je polovinou obs - Záhon 10
 Záhon tvaru dvou rovnostranných trojúhelníků se společnou stranou, s délkou strany 2,5 m má být osázen sazenicemi okrasného keře. Zahradník doporučil mezi jednotlivými sazenicemi ponechat mezery 40 cm a na samotnou sazenici je potřeba 10 cm z obvodu. Urči
Záhon tvaru dvou rovnostranných trojúhelníků se společnou stranou, s délkou strany 2,5 m má být osázen sazenicemi okrasného keře. Zahradník doporučil mezi jednotlivými sazenicemi ponechat mezery 40 cm a na samotnou sazenici je potřeba 10 cm z obvodu. Urči - Lichoběžník
 V rovnoramenného lichoběžníku KLMN je průsečík úhlopříček označen písmenem S. Vypočítejte obsah lichoběžníku, pokud /KS/: /SM/ = 2:1 a obsah trojúhelníku KSN je 14 cm².
V rovnoramenného lichoběžníku KLMN je průsečík úhlopříček označen písmenem S. Vypočítejte obsah lichoběžníku, pokud /KS/: /SM/ = 2:1 a obsah trojúhelníku KSN je 14 cm². - Pětiúhelník
 Vypočítejte obsah pravidelného pětiúhelníku, jehož úhlopříčka je dlouhá u=20.
Vypočítejte obsah pravidelného pětiúhelníku, jehož úhlopříčka je dlouhá u=20. - Pravoúhlý 37
 Pravoúhlý trojúhelník má obsah 36 cm². V něm je umístěn čtverec tak, že dvě strany čtverce jsou částmi dvou stran trojúhelníku a jeden vrchol čtverce je ve třetině nejdelší strany. Určete obsah tohoto čtverce.
Pravoúhlý trojúhelník má obsah 36 cm². V něm je umístěn čtverec tak, že dvě strany čtverce jsou částmi dvou stran trojúhelníku a jeden vrchol čtverce je ve třetině nejdelší strany. Určete obsah tohoto čtverce. - Černé stavby
 Jozef postavil stavbu s obdélníkového půdorysu 5 m × 5,2 m. Vypočítejte o kolik procent překročil limit 25 m² na drobnou stavbu. Stavba která není postavena v souladu se zákonem se nazývá "černá stavba". Vypočítejte úhel, který by měly stěny stavby navzáj
Jozef postavil stavbu s obdélníkového půdorysu 5 m × 5,2 m. Vypočítejte o kolik procent překročil limit 25 m² na drobnou stavbu. Stavba která není postavena v souladu se zákonem se nazývá "černá stavba". Vypočítejte úhel, který by měly stěny stavby navzáj - Lichoběžník 83
 Lichoběžník ABCD je složen z pěti trojúhelníků. Body E, G dělí úsečku AB v poměru 2:4:3 (v tomto pořadí) na tři úsečky. Bod F je středem úsečky AD. Trojúhelník AEF je rovnoramenný a pravoúhlý. Trojúhelníky GBC a CDG jsou pravoúhlé. Obsah trojúhelníku AEF
Lichoběžník ABCD je složen z pěti trojúhelníků. Body E, G dělí úsečku AB v poměru 2:4:3 (v tomto pořadí) na tři úsečky. Bod F je středem úsečky AD. Trojúhelník AEF je rovnoramenný a pravoúhlý. Trojúhelníky GBC a CDG jsou pravoúhlé. Obsah trojúhelníku AEF - Obdélník ABCD
 Obdélník ABCD, jehož |AB| = 5cm, |AC| = 8 cm, ∢ |CAB| = 30°. Jak dlouhá je druhá strana a jaký je jeho obsah?
Obdélník ABCD, jehož |AB| = 5cm, |AC| = 8 cm, ∢ |CAB| = 30°. Jak dlouhá je druhá strana a jaký je jeho obsah? - MO Z8–I–6 2018
 V lichoběžníku KLMN má základna KL velikost 40 cm a základna MN má velikost 16 cm. Bod P leží na úsečce KL tak, že úsečka NP rozděluje lichoběžník na dvě části se stejnými obsahy. Určete velikost úsečky KP.
V lichoběžníku KLMN má základna KL velikost 40 cm a základna MN má velikost 16 cm. Bod P leží na úsečce KL tak, že úsečka NP rozděluje lichoběžník na dvě části se stejnými obsahy. Určete velikost úsečky KP. - Tulipány
 Dobrákovi pěstovali tulipány na čtvercovém záhonku o straně 6 metrů. Později přistavěli k svému domku čtvercovou terasu se stranou 7 metrů. Jeden vrchol terasy ležel přesně uprostřed tulipánového záhonu a jedna strana terasy dělila stranu tulipánového záh
Dobrákovi pěstovali tulipány na čtvercovém záhonku o straně 6 metrů. Později přistavěli k svému domku čtvercovou terasu se stranou 7 metrů. Jeden vrchol terasy ležel přesně uprostřed tulipánového záhonu a jedna strana terasy dělila stranu tulipánového záh - Obsah a úhly
 Vypočítej velikosti všech stran a vnitřních úhlů trojúhelníku ABC, jestliže je dáno: S = 501,9; α = 15°28' a β = 45°.
Vypočítej velikosti všech stran a vnitřních úhlů trojúhelníku ABC, jestliže je dáno: S = 501,9; α = 15°28' a β = 45°. - Obdélník 3-4-5
 Délky stran obdélníka jsou v poměru 3:4. Délka úhlopříčky obdélníka je 20 cm. Výpočtěte obsah obdélníka.
Délky stran obdélníka jsou v poměru 3:4. Délka úhlopříčky obdélníka je 20 cm. Výpočtěte obsah obdélníka. - MO Z9 2019 domace kolo
 V trojúhelníku ABC leží bod P ve třetině úsečky AB blíže bodu A, bod R je ve třetině úsečky P B blíže bodu P a bod Q leží na úsečce BC tak, že úhly P CB a RQB jsou shodné. Určete poměr obsahů trojúhelníků ABC a PQC.
V trojúhelníku ABC leží bod P ve třetině úsečky AB blíže bodu A, bod R je ve třetině úsečky P B blíže bodu P a bod Q leží na úsečce BC tak, že úhly P CB a RQB jsou shodné. Určete poměr obsahů trojúhelníků ABC a PQC. - Trojúhelník
 Je dán trojúhelník KLM souřadnicemi vrcholů v rovině: K[0, 20] L[-12, 2] M[17, -11]. Vypočítejte jeho obsah a vnitřní úhly.
Je dán trojúhelník KLM souřadnicemi vrcholů v rovině: K[0, 20] L[-12, 2] M[17, -11]. Vypočítejte jeho obsah a vnitřní úhly. - Čokoláda
 Krychle čokoládové rolády s hranou 5 cm váží 30g. Kolik kalorií v sobě bude obsahovat ta samá čokoládová roláda tvaru hranolu s délkou 0,5 m, jejíž průřez je rovnoramenný lichoběžník se základnami 25 a 13 cm a rameny 10 cm. Víte, že ve 100 g této rolády j
Krychle čokoládové rolády s hranou 5 cm váží 30g. Kolik kalorií v sobě bude obsahovat ta samá čokoládová roláda tvaru hranolu s délkou 0,5 m, jejíž průřez je rovnoramenný lichoběžník se základnami 25 a 13 cm a rameny 10 cm. Víte, že ve 100 g této rolády j - Uhlopříčky 19
 Určete délky uhlopříček kosočtverce, je-li obsah 156 cm² a strana 13 cm.
Určete délky uhlopříček kosočtverce, je-li obsah 156 cm² a strana 13 cm.
Máš úkol, který jsi tady nenašel vyřešen? Pošli nám úkol a my Ti ji zkusíme vypočítat. Řešení příkladů z matematiky.
