Příklady na obsah trojúhelníka - strana 28 z 45
Počet nalezených příkladů: 882
- Z7–I–2 MO 2017
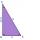 Jsou dány dvě dvojice rovnoběžných přímek AB k CD a AC k BD. Bod E leží na přímce BD, bod F je středem úsečky BD, bod G je středem úsečky CD a obsah trojúhelníku ACE je 20 cm². Určete obsah trojúhelníku DFG.
Jsou dány dvě dvojice rovnoběžných přímek AB k CD a AC k BD. Bod E leží na přímce BD, bod F je středem úsečky BD, bod G je středem úsečky CD a obsah trojúhelníku ACE je 20 cm². Určete obsah trojúhelníku DFG. - V lichoběžníku
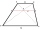 V lichoběžníku ABCD jsou dány základny: AB = 12cm CD = 4 cm A úhlopříčky se protínají pod pravým úhlem. Jaký je obsah tohoto lichoběžníku ABCD?
V lichoběžníku ABCD jsou dány základny: AB = 12cm CD = 4 cm A úhlopříčky se protínají pod pravým úhlem. Jaký je obsah tohoto lichoběžníku ABCD? - Valec naležato
 Válec o průměru 3m a výšce/délce 15 m je položen naležato. Je do něj napuštěna voda, která sahá do výšky 60 cm pod osu válce. Kolik hektolitrů vody je ve válci?
Válec o průměru 3m a výšce/délce 15 m je položen naležato. Je do něj napuštěna voda, která sahá do výšky 60 cm pod osu válce. Kolik hektolitrů vody je ve válci? - Trojboký jehlan
 Vypočítejte objem a povrch pravidelného trojbokého jehlanu, jehož výška je stejná jako délka hrany podstavy 10 cm.
Vypočítejte objem a povrch pravidelného trojbokého jehlanu, jehož výška je stejná jako délka hrany podstavy 10 cm. - Pravoúhlý lichoběžník
 Uveden je pravoúhlý lichoběžník s mírou ostrého úhlu 50°. Délka jeho podstavců je 4 a 6 jednotek. Objem pevné látky získaný rotací daného lichoběžníku kolem delší základny je:
Uveden je pravoúhlý lichoběžník s mírou ostrého úhlu 50°. Délka jeho podstavců je 4 a 6 jednotek. Objem pevné látky získaný rotací daného lichoběžníku kolem delší základny je: - Malovka
 Kolik Kč zaplatíte za výmalbu pokoje tvaru kvádru s rozměry podlahy 5 a 4m, když výška pokoje je 3 m. Nebudete malovat podlahu, prostor dveří (210 x 90 cm) a prostor za zrcadlem (rovnostranný trojúhelník se stranou 4 dm). Chcete udělat dvojitý nátěr, vyda
Kolik Kč zaplatíte za výmalbu pokoje tvaru kvádru s rozměry podlahy 5 a 4m, když výška pokoje je 3 m. Nebudete malovat podlahu, prostor dveří (210 x 90 cm) a prostor za zrcadlem (rovnostranný trojúhelník se stranou 4 dm). Chcete udělat dvojitý nátěr, vyda - Kornout
 Kolik cm² těsta je třeba na výrobu zmrzlinového kornoutu, má-li se do něj vejít 0,3l zmrzliny a jeho výška má být 15 cm. Připočti 8% na přehyby. 1. Převeď litry na cm³ 2. Rozhodni, jaký údaj můžeš dopočítat jako první a z jakého vzorce. 3. Vypočítej údaj
Kolik cm² těsta je třeba na výrobu zmrzlinového kornoutu, má-li se do něj vejít 0,3l zmrzliny a jeho výška má být 15 cm. Připočti 8% na přehyby. 1. Převeď litry na cm³ 2. Rozhodni, jaký údaj můžeš dopočítat jako první a z jakého vzorce. 3. Vypočítej údaj - Koule ve kuželi
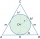 Do kužele je vepsána koule (průnik jejich hranic se skládá z kružnice a jednoho bodu). Poměr povrchu koule a obsahu podstavy je 4:3. Rovina, která prochází osou kužele, řeže kužel v rovnoramenném trojúhelníku. Určete velikost úhlu oproti základně tohoto t
Do kužele je vepsána koule (průnik jejich hranic se skládá z kružnice a jednoho bodu). Poměr povrchu koule a obsahu podstavy je 4:3. Rovina, která prochází osou kužele, řeže kužel v rovnoramenném trojúhelníku. Určete velikost úhlu oproti základně tohoto t - Komolý jehlan
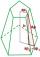 Vypočtěte objem pravidelného šestibokého komolého jehlanu, jestliže je délka hrany dolní podstavy 30 cm, horní podstavy 12 cm a pokud délka boční hrany je 41 cm.
Vypočtěte objem pravidelného šestibokého komolého jehlanu, jestliže je délka hrany dolní podstavy 30 cm, horní podstavy 12 cm a pokud délka boční hrany je 41 cm. - 4-boký jehlan v2
 Vypočítejte objem a povrch pravidelného čtyřbokého jehlanu, jeli obsah podstavy 20 cm². Odchylka boční hrany od roviny podstavy je 60 stupňů.
Vypočítejte objem a povrch pravidelného čtyřbokého jehlanu, jeli obsah podstavy 20 cm². Odchylka boční hrany od roviny podstavy je 60 stupňů. - 3b hranol
 Vypočítej obsah pláště pravidelného trojbokého hranolu, je-li délka jeho podstavné hrany 6,5 cm a výška 0,2m.
Vypočítej obsah pláště pravidelného trojbokého hranolu, je-li délka jeho podstavné hrany 6,5 cm a výška 0,2m. - Vrchol 9
 Vrchol věže má tvar pravidelného šestibokého jehlanu. Podstavná hrana má délku 1,2 m, výška jehlanu je 1,6 m. Kolik metrů čtverečných plechu je potřeba na pokrytí vrcholu věže, je-li na spoje, překrytí a odpad zapotřebí 15% plechu navíc?
Vrchol věže má tvar pravidelného šestibokého jehlanu. Podstavná hrana má délku 1,2 m, výška jehlanu je 1,6 m. Kolik metrů čtverečných plechu je potřeba na pokrytí vrcholu věže, je-li na spoje, překrytí a odpad zapotřebí 15% plechu navíc? - Trojboký hranol 8
 Jen dán pravidelný trojboký hranol s hranou podstavy 20dm a výškou 30dm. Vypočítejte objem hranolu a obsah pláště.
Jen dán pravidelný trojboký hranol s hranou podstavy 20dm a výškou 30dm. Vypočítejte objem hranolu a obsah pláště. - Čtyřboký hranol
 Vypočítejte povrch a objem čtyřbokého hranolu, který má podstavu tvaru kosodélníka, pokud jeho rozměry jsou: a = 12cm, b = 7cm, Va = 6cm a výška hranolu h = 10cm.
Vypočítejte povrch a objem čtyřbokého hranolu, který má podstavu tvaru kosodélníka, pokud jeho rozměry jsou: a = 12cm, b = 7cm, Va = 6cm a výška hranolu h = 10cm. - Karnevalova čepice
 Kolik dm² ozdobného papíru je potřeba ke zhotovení karnevalových čepic tvaru kužele pro 46 prvňáků, pokud obvod hlavy prvňáčka je 49 cm a výška čepice má být 33 cm. Na záhyby je nutné přidat 3% papíru?
Kolik dm² ozdobného papíru je potřeba ke zhotovení karnevalových čepic tvaru kužele pro 46 prvňáků, pokud obvod hlavy prvňáčka je 49 cm a výška čepice má být 33 cm. Na záhyby je nutné přidat 3% papíru? - Kužel
 Vypočítej objem a povrch kužele, pokud průměr podstavy je d = 14 cm a strana kužele svírá s rovinou podstavy úhel 34°24'.
Vypočítej objem a povrch kužele, pokud průměr podstavy je d = 14 cm a strana kužele svírá s rovinou podstavy úhel 34°24'. - Dovolená - stan
 Ivan a Katka objevili na dovolené pravidelný jehlan, jehož podstavou byl čtverec se stranou 230 m a jehož výška byla rovna poloměru kruhu se stejným obsahem jako podstavný čtverec. Katka označila vrcholy čtverce ABCD. Ivan vyznačil na přímce spojující bod
Ivan a Katka objevili na dovolené pravidelný jehlan, jehož podstavou byl čtverec se stranou 230 m a jehož výška byla rovna poloměru kruhu se stejným obsahem jako podstavný čtverec. Katka označila vrcholy čtverce ABCD. Ivan vyznačil na přímce spojující bod - Dřevená 3
 Dřevená deska dlouhá 2,5m má pruřez tvaru pravidelného lichobežníku jehož rovnobežné strany májí delku 1,2dm a 8cm vyška lichobežníka je 3cm. Vypočtete: a) povrch desky pro vypočet spotřeby mořidla b) hmotnost desky je-li hustota dřeva je 600kg/m³ c) koli
Dřevená deska dlouhá 2,5m má pruřez tvaru pravidelného lichobežníku jehož rovnobežné strany májí delku 1,2dm a 8cm vyška lichobežníka je 3cm. Vypočtete: a) povrch desky pro vypočet spotřeby mořidla b) hmotnost desky je-li hustota dřeva je 600kg/m³ c) koli - Věžička
 Věžička má tvar pravidelného čtyřbokého jehlanu s podstavnou hranou délky 0,8 m. Výška věžičky je 1,2 m. Kolik metrů čtverečných je potřeba na její pokrytí, počítáne-li na odpad 10% plechu navíc.
Věžička má tvar pravidelného čtyřbokého jehlanu s podstavnou hranou délky 0,8 m. Výška věžičky je 1,2 m. Kolik metrů čtverečných je potřeba na její pokrytí, počítáne-li na odpad 10% plechu navíc. - Věžička 2
 Věžička má půdorys tvaru čtverce s délkou strany 5m. Střecha věžičky má tvar pravidelného čtyřbokého jehlanu (bez podstavy) s výškou 8m. Při rekonstrukci se bude střecha pokrývat novými taškami. Na 1 m² se spotřebuje 11 tašek. Na jedné paletě je uskladněn
Věžička má půdorys tvaru čtverce s délkou strany 5m. Střecha věžičky má tvar pravidelného čtyřbokého jehlanu (bez podstavy) s výškou 8m. Při rekonstrukci se bude střecha pokrývat novými taškami. Na 1 m² se spotřebuje 11 tašek. Na jedné paletě je uskladněn
Máš úkol, který jsi tady nenašel vyřešen? Pošli nám úkol a my Ti ji zkusíme vypočítat. Řešení příkladů z matematiky.
