Dovolená - stan
Ivan a Katka objevili na dovolené pravidelný jehlan, jehož podstavou byl čtverec se stranou 230 m a jehož výška byla rovna poloměru kruhu se stejným obsahem jako podstavný čtverec. Katka označila vrcholy čtverce ABCD. Ivan vyznačil na přímce spojující bod B s vrcholem jehlanu takový bod E, že délka lomené čáry AEC byla nejkratší možná. Určete délku lomené čáry AEC zaokrouhlenou na celé centimetry.
Správná odpověď:
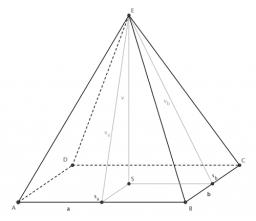
Tipy na související online kalkulačky
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
algebraaritmetikastereometrieplanimetriezákladní operace a pojmyÚroveň náročnosti úkolu
Související a podobné příklady:
- Výška jehlanu
 Podstava hranolu má tvar čtverce se stranou 10 cm. Výška hranolu je 20 cm. Vypočítejte výšku jehlanu s podstavou tvaru čtverce o straně 10 cm, který má čtyřikrát menší objem než hranol.
Podstava hranolu má tvar čtverce se stranou 10 cm. Výška hranolu je 20 cm. Vypočítejte výšku jehlanu s podstavou tvaru čtverce o straně 10 cm, který má čtyřikrát menší objem než hranol. - Obvod 34
 Obvod podstavy pravidelného čtyřbokého jehlanu je stejně velký jako jeho výška. Jehlan má objem 288 dm³. Vypočítejte jeho povrch. Výsledek zaokrouhlete na celé dm².
Obvod podstavy pravidelného čtyřbokého jehlanu je stejně velký jako jeho výška. Jehlan má objem 288 dm³. Vypočítejte jeho povrch. Výsledek zaokrouhlete na celé dm². - Kvadratura kruhu
 Výpočtem určitě stranu čtverce se stejným obsahem jako kruh o poloměru 17.
Výpočtem určitě stranu čtverce se stejným obsahem jako kruh o poloměru 17. - Desaťuholník - hranol
 Pravidelný desaťuholník se stranou a = 2 cm je podstavou kolmého hranolu, jehož boční stěny jsou čtverce. Určete objem hranolu v cm³ s přesností na dvě desetinná místa.
Pravidelný desaťuholník se stranou a = 2 cm je podstavou kolmého hranolu, jehož boční stěny jsou čtverce. Určete objem hranolu v cm³ s přesností na dvě desetinná místa. - Strana
 Vypočítejte velikost strany čtverce ABCD s vrcholem A [0, 0], pokud úhlopříčka BD leží na přímce p: -4x -5 =0.
Vypočítejte velikost strany čtverce ABCD s vrcholem A [0, 0], pokud úhlopříčka BD leží na přímce p: -4x -5 =0. - Trojúhelník konšt.
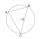 Narýsuj kružnici k(S, r=3cm). Sestroj trojúhelník ABC tak , aby jeho vrcholy ležely na kružnici k a délka stran byla (AB)=2,5cm (AC)=4cm
Narýsuj kružnici k(S, r=3cm). Sestroj trojúhelník ABC tak , aby jeho vrcholy ležely na kružnici k a délka stran byla (AB)=2,5cm (AC)=4cm - Lichoběžník 21
 Je dán lichoběžníku ABCD s rovnoběžnými stranami AB a CD pro bod E strany AB plati, že úsečka DE dělí lichoběžník na dvě části se stejným obsahem. Spočítej délku úsečky AE.
Je dán lichoběžníku ABCD s rovnoběžnými stranami AB a CD pro bod E strany AB plati, že úsečka DE dělí lichoběžník na dvě části se stejným obsahem. Spočítej délku úsečky AE.
