Příklady na trojúhelník - strana 90 z 124
Počet nalezených příkladů: 2480
- Objem válce
 Osovým řezem válce je obdélník s úhlopříčkou u = 20 cm. Výška válce je dvakrát větší než průměr podstavy. Vypočítejte objem válce v litrech.
Osovým řezem válce je obdélník s úhlopříčkou u = 20 cm. Výška válce je dvakrát větší než průměr podstavy. Vypočítejte objem válce v litrech. - Obvod a obsah
 Vypočítejte obvod a obsah čtverce s délkou úhlopříčky 30 cm.
Vypočítejte obvod a obsah čtverce s délkou úhlopříčky 30 cm. - Tunel - čtyřúhelník
 Jak dlouhý bude tunel AB, vzdálenosti AD=35 m, DC=120 m, CB=85 m a úhly ADC=105 stupňů a BCD=71 stupňů. ABCD je čtyřúhelník.
Jak dlouhý bude tunel AB, vzdálenosti AD=35 m, DC=120 m, CB=85 m a úhly ADC=105 stupňů a BCD=71 stupňů. ABCD je čtyřúhelník. - Objem a povrch kvádru s výřezem
 Vypočítej objem a povrch tělesa, které vznikne tak, že z kvádru o rozměrech 10 cm 15 cm a 20 cm vyřízneme trojboký hranol se stejnou výškou, jehož podstava je pravoúhlý trojúhelník o rozměrech 3 cm , 4 cm a 5 cm
Vypočítej objem a povrch tělesa, které vznikne tak, že z kvádru o rozměrech 10 cm 15 cm a 20 cm vyřízneme trojboký hranol se stejnou výškou, jehož podstava je pravoúhlý trojúhelník o rozměrech 3 cm , 4 cm a 5 cm - Obvod a obsah lichobežníku
 V rovnoramennom lichobežníku sú délky základní 15cm a 9cm. Uhlopriečky mají délku 13cm. Vypočítajte obvod a obsah lichobežníku.
V rovnoramennom lichobežníku sú délky základní 15cm a 9cm. Uhlopriečky mají délku 13cm. Vypočítajte obvod a obsah lichobežníku. - Obsah rovnoramenného lichoběžníku
 V rovnoramenném lichoběžníku ABCD známe: AB||CD, |CD| = c = 8 cm, výška h = 7 cm, | CAB| = 35°. Najděte obsah lichoběžníku.
V rovnoramenném lichoběžníku ABCD známe: AB||CD, |CD| = c = 8 cm, výška h = 7 cm, | CAB| = 35°. Najděte obsah lichoběžníku. - Délka RRL
 Jaká je délka (obvod) rovnoramenného lichoběžníku, ve kterém jsou dány délky jeho základen a výšky? a = 8cm c = 2cm v = 4cm
Jaká je délka (obvod) rovnoramenného lichoběžníku, ve kterém jsou dány délky jeho základen a výšky? a = 8cm c = 2cm v = 4cm - Hranol 4b-pravidelný
 Vypočítejte objem a povrch pravidelného čtyřbokého hranolu jehož výška je 28,6cm a tělesová úhlopříčka svírá s rovinou podstavy úhel 50 stupnů.
Vypočítejte objem a povrch pravidelného čtyřbokého hranolu jehož výška je 28,6cm a tělesová úhlopříčka svírá s rovinou podstavy úhel 50 stupnů. - Dva přátelé
 Dva přátelé mají k dispozici krátkovlnné vysílačky s dosahem 13 km. První z nich jede vlakem rychlostí 48km za hodinu po přímém úseku trati, od kterého je druhý z přátel vzdálen 5km. Jak dlouhou dobu bude pro oba přátele umožněno rádiové spojení?
Dva přátelé mají k dispozici krátkovlnné vysílačky s dosahem 13 km. První z nich jede vlakem rychlostí 48km za hodinu po přímém úseku trati, od kterého je druhý z přátel vzdálen 5km. Jak dlouhou dobu bude pro oba přátele umožněno rádiové spojení? - Černé stavby
 Jozef postavil stavbu s obdélníkového půdorysu 5 m × 5,2 m. Vypočítejte o kolik procent překročil limit 25 m² na drobnou stavbu. Stavba která není postavena v souladu se zákonem se nazývá "černá stavba". Vypočítejte úhel, který by měly stěny stavby navzáj
Jozef postavil stavbu s obdélníkového půdorysu 5 m × 5,2 m. Vypočítejte o kolik procent překročil limit 25 m² na drobnou stavbu. Stavba která není postavena v souladu se zákonem se nazývá "černá stavba". Vypočítejte úhel, který by měly stěny stavby navzáj - Vepsaná kruhu
 Napište rovnici kružnice vepsané trojúhelníku KLM, je-li K[ 2,1], L[6,4], M[6,1].
Napište rovnici kružnice vepsané trojúhelníku KLM, je-li K[ 2,1], L[6,4], M[6,1]. - Obsah rovnoběžníku z úhlopříček
 Vypočítejte obsah rovnoběžníku, pokud jsou velikosti stran a=80, b=60 a velikost úhlu sevřeného úhlopříčkami je 60°.
Vypočítejte obsah rovnoběžníku, pokud jsou velikosti stran a=80, b=60 a velikost úhlu sevřeného úhlopříčkami je 60°. - Kosodélník
 Konstrukce kosodélníku ABCD, zadáno: a+b=9 cm; AC=4,5 cm; výška ha=3,5 cm Kolik měří strany a a b?
Konstrukce kosodélníku ABCD, zadáno: a+b=9 cm; AC=4,5 cm; výška ha=3,5 cm Kolik měří strany a a b? - Úhlopříčky kosočtverce z obvodu
 Jak zjistím úhlopříčky kosočtverce, pokud jeho obvod je 80dm a jedna úhlopříčka je 2x větší než druhá?
Jak zjistím úhlopříčky kosočtverce, pokud jeho obvod je 80dm a jedna úhlopříčka je 2x větší než druhá? - Půlkruh
 V půlkruhu se středem S a průměrem AB je sestrojen rovnostranný trojúhelník SBC. Jaká je velikost úhlu ∠ SAC?
V půlkruhu se středem S a průměrem AB je sestrojen rovnostranný trojúhelník SBC. Jaká je velikost úhlu ∠ SAC? - Lichoběžník 26
 V rovnoramenném lichoběžníku ABCD vypočítej chybějící délku strany "a" a pak jeho obsah. Strana b=d=50 cm, c=20 cm, výška=48 cm.
V rovnoramenném lichoběžníku ABCD vypočítej chybějící délku strany "a" a pak jeho obsah. Strana b=d=50 cm, c=20 cm, výška=48 cm. - RR lichoběžník v2
 Základny RR (rovnoramenného) lichoběžníku měří 15 cm a 2 cm, jeho obvod je 38 cm. Jaký obsah má lichoběžník?
Základny RR (rovnoramenného) lichoběžníku měří 15 cm a 2 cm, jeho obvod je 38 cm. Jaký obsah má lichoběžník? - Zemekoule
 Kolik procent zemského povrchu leží v pásmu tropickém, mírném, arktickém? Hranici mezi pásmy tvoří rovnoběžky 23°27' a 66°33'.
Kolik procent zemského povrchu leží v pásmu tropickém, mírném, arktickém? Hranici mezi pásmy tvoří rovnoběžky 23°27' a 66°33'. - Čtverec ABCD
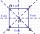 Je dán čtverec ABCD s délkou strany 100 mm. Vypočítej poloměr kružnice, která prochází vrcholy B, C a středem strany AD.
Je dán čtverec ABCD s délkou strany 100 mm. Vypočítej poloměr kružnice, která prochází vrcholy B, C a středem strany AD. - Úhlopříčky
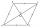 Jedna úhlopříčka kosočtverce je větší než druhá o 4 cm. Pokud je plocha kosočtverce 96 cm2, najděte stranu kosočtverce.
Jedna úhlopříčka kosočtverce je větší než druhá o 4 cm. Pokud je plocha kosočtverce 96 cm2, najděte stranu kosočtverce.
Máš úkol, který jsi tady nenašel vyřešen? Pošli nám úkol a my Ti ji zkusíme vypočítat. Řešení příkladů z matematiky.
