Hranol 4b-pravidelný
Vypočítejte objem a povrch pravidelného čtyřbokého hranolu jehož výška je 28,6 cm a tělesová úhlopříčka svírá s rovinou podstavy úhel 50 stupnů.
Vaše odpověď:
Vaše odpověď:
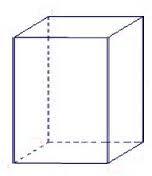
Tipy na související online kalkulačky
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Víte objem a jednotku objemu a chcete proměnit jednotku objemu?
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte si převody jednotek úhlů úhlové stupně, minuty, sekundy, radiány.
Víte objem a jednotku objemu a chcete proměnit jednotku objemu?
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte si převody jednotek úhlů úhlové stupně, minuty, sekundy, radiány.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
algebraaritmetikastereometrieplanimetriegoniometrie a trigonometrieJednotky fyzikálních veličinÚroveň náročnosti úkolu
Související a podobné příklady:
- Úhlopříčka
Tělesová úhlopříčka pravidelného čtyřbokého hranolu svírá s podstavou úhel 60 stupňů, délka hrany postavy je 10 cm. Jaký je objem tělesa? - Tělesová
Tělesová úhlopříčka pravidelného čtyřbokého hranolu svírá s podstavou úhel velikosti 60°. Hrana podstavy má délku 10 cm. Vypočítejte objem tělesa. - Vypočítejte 4BH
Vypočítejte objem a povrch pravidelného čtyřbokého hranolu o podstavné hraně a=24 cm, jestliže tělesová úhlopříčka svírá s podstavou úhel 66° - Spádnice
Určit objem a povrch kužele, jehož spádnice o délce 8 cm svírá s rovinou podstavy úhel 75 stupňů - Čtyřboký hranol
Vypočítejte povrch pravidelného čtyřbokého hranolu, jehož hrana podstavy je 2,4dm a výška hranolu je 38cm. - Vypočítej 39
Vypočítej objem (V) a povrch (S) pravidelného čtyřbokého hranolu, jehož výška je 28,6 cm a odchylka tělesové úhlopříčky od roviny podlahy je 50°. - Hranol 4b 2
Tělesová úhlopříčka pravidelného čtyřbokého hranolu svírá s podstavou úhel 60°. Hrana podstavy má délku 20 cm. Vypočtěte objem tělesa.
