Úhel - střední škola - příklady a úlohy
Počet nalezených příkladů: 530
- V trojúhelníku 7
 V trojúhelníku ABC svírají osy úhlů alpha a beta úhel fí = R + gama/2. R je pravý úhel 90°. Ověřte.
V trojúhelníku ABC svírají osy úhlů alpha a beta úhel fí = R + gama/2. R je pravý úhel 90°. Ověřte. - Užitím 2
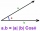
 Užitím kosinové věty dokažte, že v rovnoramenném trojúhelníku ABC se základnou AB platí, že c=2a cos α.
Užitím kosinové věty dokažte, že v rovnoramenném trojúhelníku ABC se základnou AB platí, že c=2a cos α. - Vypočítej 400
 Vypočítej vnitřní úhly trojúhelníku. Úhel alfa je o 16° větší než beta a úhel gama je o 17° menší než alfa.
Vypočítej vnitřní úhly trojúhelníku. Úhel alfa je o 16° větší než beta a úhel gama je o 17° menší než alfa. - Tři kamarádi 8
 Tři kamarádi sedí na molu, které je přesně uprostřed tekoucí řeky. prvni kamarád se vydává proti proudu řeky rychlostí 0,4 m/s, druhý kamarád se vydává po proudu řeky rychlostí 0,2 m/s, třetí kamarád pluje kolmo směrem ke břehu rychlostí 0,8 m/s. Rychlost
Tři kamarádi sedí na molu, které je přesně uprostřed tekoucí řeky. prvni kamarád se vydává proti proudu řeky rychlostí 0,4 m/s, druhý kamarád se vydává po proudu řeky rychlostí 0,2 m/s, třetí kamarád pluje kolmo směrem ke břehu rychlostí 0,8 m/s. Rychlost
- V trojúhelníku 8
 V trojúhelníku ABC znáte poměr délek stran a:b:c=3:4:6. Vypočítejte velikosti úhlů trojúhelníku ABC.
V trojúhelníku ABC znáte poměr délek stran a:b:c=3:4:6. Vypočítejte velikosti úhlů trojúhelníku ABC. - V obecném
 V obecném čtyřúhelníku ABCD je úhel β o 9° větší než úhel α, úhel γ je o 24° větší než úhel α a úhel δ je o 50° větší než úhel β. Urči velikosti jednotlivých úhlů.
V obecném čtyřúhelníku ABCD je úhel β o 9° větší než úhel α, úhel γ je o 24° větší než úhel α a úhel δ je o 50° větší než úhel β. Urči velikosti jednotlivých úhlů. - Těžnice 10
 Je dána úsečka AA1 délky 6 cm. Sestrojte všechny trojúhelníky ABC, pro které je AA1 těžnicí, délka strany BC je 5 cm a velikost úhlu gama je 60°.
Je dána úsečka AA1 délky 6 cm. Sestrojte všechny trojúhelníky ABC, pro které je AA1 těžnicí, délka strany BC je 5 cm a velikost úhlu gama je 60°. - V rovině 2
 V rovině je umístěn trojúhelník ABC s pravým úhlem u vrcholu C, pro který platí: A(1, 2), B(5, 2), C(x, x+1), kde x > -1. a) určete hodnotu x b) určete souřadnice bodu M, který je středem úsečky AB c) dokažte že vektory AB a CM jsou kolmé d) určete vel
V rovině je umístěn trojúhelník ABC s pravým úhlem u vrcholu C, pro který platí: A(1, 2), B(5, 2), C(x, x+1), kde x > -1. a) určete hodnotu x b) určete souřadnice bodu M, který je středem úsečky AB c) dokažte že vektory AB a CM jsou kolmé d) určete vel - Triangulace - výškové úhly
 Vrchol věže stojící na rovině vidíme z určitého místa A ve výškovém úhlu 39° 25´. Přijdeme-li směrem k jeho patě o 50m blíže na místo B, vidíme z něho vrchol věže ve výškovém úhlu 56° 42´. Jak vysoká je věž?
Vrchol věže stojící na rovině vidíme z určitého místa A ve výškovém úhlu 39° 25´. Přijdeme-li směrem k jeho patě o 50m blíže na místo B, vidíme z něho vrchol věže ve výškovém úhlu 56° 42´. Jak vysoká je věž?
- Tramvajová úloha
 Jaký je maximální úhel pod kterým může jet tramvaj z kopce dolů, aby stále byla schopna zastavit. Součinitel smykového tření je f =0,15.
Jaký je maximální úhel pod kterým může jet tramvaj z kopce dolů, aby stále byla schopna zastavit. Součinitel smykového tření je f =0,15. - Z rozhledně
 Z rozhledně vysoké 40 m je vidět vrchol topolu pod hloubkovym uhlem o velikosti 50*10´a patu topolu v hloubkovem úhlu o velikosti 58*. Vypocitejte výšku topolu.
Z rozhledně vysoké 40 m je vidět vrchol topolu pod hloubkovym uhlem o velikosti 50*10´a patu topolu v hloubkovem úhlu o velikosti 58*. Vypocitejte výšku topolu. - Triangulace
 Zjisti výšku věže, když bylo naměřeno α=34° 30´ β=41°. Vzdálenost míst AB je 14 metrů.
Zjisti výšku věže, když bylo naměřeno α=34° 30´ β=41°. Vzdálenost míst AB je 14 metrů. - Trojuhelníku 135
 Trojuhelníku ABC o stranách a = 15 cm, b = 17,4 cm, c = 21,6 cm je opsána kružnice. Vypočítejte obsah úsečí určených stranami trojúhelníku.
Trojuhelníku ABC o stranách a = 15 cm, b = 17,4 cm, c = 21,6 cm je opsána kružnice. Vypočítejte obsah úsečí určených stranami trojúhelníku. - Radiány - porovnávání
 Co je větší úhel? -0,7 radiánov nebo -0,7π radiánov?
Co je větší úhel? -0,7 radiánov nebo -0,7π radiánov?
- Kvadrant
 Ve kterém kvadrantu leží úhel -1165°?
Ve kterém kvadrantu leží úhel -1165°? - Argument 41981
 Najděte mod z a argument z, pokud z=i
Najděte mod z a argument z, pokud z=i - Najděte
 Najděte vektor v4 kolmý na vektory v1 = (1, 1, 1, -1), v2 = (1, 1, -1, 1) a v3 = (0, 0, 1, 1)
Najděte vektor v4 kolmý na vektory v1 = (1, 1, 1, -1), v2 = (1, 1, -1, 1) a v3 = (0, 0, 1, 1) - Určete 11
 Určete mezný úhel pro dvojici prostředí diamant- vzduch. n_d = 2,42 α_m =? Absolutní index lomu světla pro vzduch n=1
Určete mezný úhel pro dvojici prostředí diamant- vzduch. n_d = 2,42 α_m =? Absolutní index lomu světla pro vzduch n=1 - Skalární součin
 Vypočítejte u.v když |v| = 5, |v| = 2 a když vektory u, v, svírají úhel: a) 60° b) 45° c) 120°
Vypočítejte u.v když |v| = 5, |v| = 2 a když vektory u, v, svírají úhel: a) 60° b) 45° c) 120°
Máš úkol, nad kterým si lámeš alespoň 10 minut hlavu? Pošli nám úkol a my Ti ji zkusíme vypočítat.
