Úhlopříčka - slovní úlohy a příklady - strana 19 z 27
Počet nalezených příkladů: 524
- Tělesová
 Tělesová úhlopříčka pravidelného čtyřbokého hranolu svírá s podstavou úhel velikosti 60°. Hrana podstavy má délku 10cm. Vypočítejte objem tělesa.
Tělesová úhlopříčka pravidelného čtyřbokého hranolu svírá s podstavou úhel velikosti 60°. Hrana podstavy má délku 10cm. Vypočítejte objem tělesa. - Koule 24
 V krychli je naskládáno 9 shodných koulí a to tak, aby co nejvíce vyplnily objem krychle. Jakou část objemu krychle vyplní?
V krychli je naskládáno 9 shodných koulí a to tak, aby co nejvíce vyplnily objem krychle. Jakou část objemu krychle vyplní? - Hranol 4b 2
 Tělesová úhlopříčka pravidelného čtyřbokého hranolu svírá s podstavou úhel 60°. Hrana podstavy má délku 20 cm. Vypočtěte objem tělesa.
Tělesová úhlopříčka pravidelného čtyřbokého hranolu svírá s podstavou úhel 60°. Hrana podstavy má délku 20 cm. Vypočtěte objem tělesa. - Osový řez
 Osový řez válce má úhlopříčku dlouhou 37 cm, a víme, že velikost pláště a podstavy je v poměru 2:6. Vypočítejte výšku válce a poloměr podstavy.
Osový řez válce má úhlopříčku dlouhou 37 cm, a víme, že velikost pláště a podstavy je v poměru 2:6. Vypočítejte výšku válce a poloměr podstavy. - Vypočítejte 4BH
 Vypočítejte objem a povrch pravidelného čtyřbokého hranolu o podstavné hraně a=24 cm, jestliže tělesová úhlopříčka svírá s podstavou úhel 66°
Vypočítejte objem a povrch pravidelného čtyřbokého hranolu o podstavné hraně a=24 cm, jestliže tělesová úhlopříčka svírá s podstavou úhel 66° - Podstava
 Podstavou kvádru je obdélník se stranou 7,5 cm a úhlopříčkou 12,5 cm. Objem kvádru je V = 0,9 dm³. Vypočtěte povrch kvádru.
Podstavou kvádru je obdélník se stranou 7,5 cm a úhlopříčkou 12,5 cm. Objem kvádru je V = 0,9 dm³. Vypočtěte povrch kvádru. - Kosoštvorec podstava
 Ypočítejte objem a povrch hranolu, jehož podstava je kosočtverec s úhlopříčkami u1 = 13 cm, u2 = 16 cm. Výška hranolu se rovná dvojnásobku podstavové hrany.
Ypočítejte objem a povrch hranolu, jehož podstava je kosočtverec s úhlopříčkami u1 = 13 cm, u2 = 16 cm. Výška hranolu se rovná dvojnásobku podstavové hrany. - Kvádr
 Kvádr ABCDEFGH o výšce 10 cm má podstavné hrany délky 6 cm a 8 cm. Určete odchylku tělesové úhlopříčky od roviny podstavy (zaokrouhlete na stupně)
Kvádr ABCDEFGH o výšce 10 cm má podstavné hrany délky 6 cm a 8 cm. Určete odchylku tělesové úhlopříčky od roviny podstavy (zaokrouhlete na stupně) - Podstavou
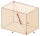 Podstavou čtyřbokého hranolu je obdélník o rozměrech 3 dm a 4 dm. Výška hranolu je 1 m. Zjistěte jaký úhel svíra tělesová úhlopříčka s úhlopříčkou podstavy.
Podstavou čtyřbokého hranolu je obdélník o rozměrech 3 dm a 4 dm. Výška hranolu je 1 m. Zjistěte jaký úhel svíra tělesová úhlopříčka s úhlopříčkou podstavy. - Kvádr - úhlopříčka
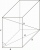 Vypočítej objem kvádru, jehož tělesova úhlopříčka u se rovná 6,1cm a obdélníková postava má rozměry 3,2cm a 2,4cm
Vypočítej objem kvádru, jehož tělesova úhlopříčka u se rovná 6,1cm a obdélníková postava má rozměry 3,2cm a 2,4cm - Hranol 23
 Hranol ABCDA'B'C'D' má čtvercovou podstavu. Stěnová úhlopříčka AC podstavy má délku 9,9cm, tělesová úhlopříčka AC' má délku 11,4cm. Vypočítejte povrch a objem hranolu.
Hranol ABCDA'B'C'D' má čtvercovou podstavu. Stěnová úhlopříčka AC podstavy má délku 9,9cm, tělesová úhlopříčka AC' má délku 11,4cm. Vypočítejte povrch a objem hranolu. - Vzdálenost bodů
 Je dán pravidelný čtyřboký jehlan ABCDV, ve kterém AB = a = 4 cm a v = 8 cm. Nechť S je střed CV. Vypočítejte vzdálenost bodů A a S.
Je dán pravidelný čtyřboký jehlan ABCDV, ve kterém AB = a = 4 cm a v = 8 cm. Nechť S je střed CV. Vypočítejte vzdálenost bodů A a S. - Poloměr válce
 Úhlopříčka osového řezu rotačního válce je 6 cm a jeho povrch je 30cm čtverečních. Vypočítej poloměr podstavy.
Úhlopříčka osového řezu rotačního válce je 6 cm a jeho povrch je 30cm čtverečních. Vypočítej poloměr podstavy. - Poměr délky úhlopříček
 Délky hran kvádru jsou v poměru 1:2:3. Budou ve stejném poměru i délky jeho stěnových úhlopříček? Kvádr má rozměry 5 cm, 10 cm a 15 cm. Vypočítejte velikost stěnových úhlopříček tohoto kvádru.
Délky hran kvádru jsou v poměru 1:2:3. Budou ve stejném poměru i délky jeho stěnových úhlopříček? Kvádr má rozměry 5 cm, 10 cm a 15 cm. Vypočítejte velikost stěnových úhlopříček tohoto kvádru. - Stěnové úhlopříčky
 Pokud jsou stěnové úhlopříčky kvádru x, y a z (diagonály), pak najděte objem kvádru. Vyřešte pro x = 1,3, y = 1, z = 1,2
Pokud jsou stěnové úhlopříčky kvádru x, y a z (diagonály), pak najděte objem kvádru. Vyřešte pro x = 1,3, y = 1, z = 1,2 - Kvádr
 Rozměry kvádru jsou v poměru 3:1:2. Tělesová úhlopříčka má délku 28cm. Vypočítejte objem kvádru.
Rozměry kvádru jsou v poměru 3:1:2. Tělesová úhlopříčka má délku 28cm. Vypočítejte objem kvádru. - Úhlopříčky kostky
 Kostka má obsah stěny 81 cm². Vypočítej délku její hrany, stěnové a tělesové úhlopříčky.
Kostka má obsah stěny 81 cm². Vypočítej délku její hrany, stěnové a tělesové úhlopříčky. - Osový řez
 Osový řez válce má úhlopříčku 23 cm. Velikost pláště a plocha podstavy jsou v poměru 6:6. Vypočtěte objem i povrch.
Osový řez válce má úhlopříčku 23 cm. Velikost pláště a plocha podstavy jsou v poměru 6:6. Vypočtěte objem i povrch. - Délky
 Délky hran kvádru jsou v poměru 2:3:6. Jeho tělesová úhlopříčka má délku 14 cm. Vypočtěte objem a povrch kvádru.
Délky hran kvádru jsou v poměru 2:3:6. Jeho tělesová úhlopříčka má délku 14 cm. Vypočtěte objem a povrch kvádru. - Sloup
 Vypočítejte objem a povrch podpůrného sloupu tvaru kolmého čtyřbokého hranolu, jehož podstavou je kosočtverec s úhlopříčku u1=102cm, u2=64cm. Výška sloupu je 1,5m.
Vypočítejte objem a povrch podpůrného sloupu tvaru kolmého čtyřbokého hranolu, jehož podstavou je kosočtverec s úhlopříčku u1=102cm, u2=64cm. Výška sloupu je 1,5m.
Máš příklad z matematiky, který jsi tady nenašel vyřešený? Pošli nám příklad a my Ti ho zkusíme vypočítat.
