Planimetrics - math word problems - page 164 of 185
Number of problems found: 3685
- Rectangular
 Rectangular triangle KLM with right angle at vertex L, angle beta at vertex K, and angle alpha at vertex M. Angle at vertex M = 65°, side l = 17.5 cm. Use Pythagorean theorems and trigonometric functions to calculate the lengths of all sides and the angle
Rectangular triangle KLM with right angle at vertex L, angle beta at vertex K, and angle alpha at vertex M. Angle at vertex M = 65°, side l = 17.5 cm. Use Pythagorean theorems and trigonometric functions to calculate the lengths of all sides and the angle - Hypotenuse and center
 Point S is the center of the hypotenuse AB of the right triangle ABC. Calculate the area of triangle ABC if the line on the hypotenuse is 0.2 dm long and if angle ∢ACS is 30°.
Point S is the center of the hypotenuse AB of the right triangle ABC. Calculate the area of triangle ABC if the line on the hypotenuse is 0.2 dm long and if angle ∢ACS is 30°. - Tree
 How tall is the tree observed at the visual angle 45°? If I stand 3 m from the tree, my eyes are two meters above the ground.
How tall is the tree observed at the visual angle 45°? If I stand 3 m from the tree, my eyes are two meters above the ground. - Binibini
 Binibini owns a triangular residential lot bounded by two roads intersecting at 70°. The sides of the lot along the road are 62m and 43m, respectively. Find the length of the fence needed to enclose the lot. (express answers to the nearest hundredths)
Binibini owns a triangular residential lot bounded by two roads intersecting at 70°. The sides of the lot along the road are 62m and 43m, respectively. Find the length of the fence needed to enclose the lot. (express answers to the nearest hundredths) - Subtracting complex in polar
 Given w =√2(cosine (pi/4) + i sine (pi/4) ) and z = 2 (cosine (pi/2) + i sine (pi/2) ). What is w - z expressed in polar form?
Given w =√2(cosine (pi/4) + i sine (pi/4) ) and z = 2 (cosine (pi/2) + i sine (pi/2) ). What is w - z expressed in polar form? - In trapezoid 3
 In a trapezoid ABCD, the elements are given - lengths of bases a= 20cm, c= 11 cm, angle α = 63°36’ and angle β=79°36’. Calculate the lengths of the other sides and the sizes of the angles.
In a trapezoid ABCD, the elements are given - lengths of bases a= 20cm, c= 11 cm, angle α = 63°36’ and angle β=79°36’. Calculate the lengths of the other sides and the sizes of the angles. - The tower
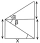 From a window 8 m above the horizontal plane, we can see the top of the tower at an elevation angle of 53 degrees 20 minutes, and its base at an angle of 14 degrees 15 minutes. How high is the tower?
From a window 8 m above the horizontal plane, we can see the top of the tower at an elevation angle of 53 degrees 20 minutes, and its base at an angle of 14 degrees 15 minutes. How high is the tower? - Centre of the hypotenuse
 The interior angles of the triangle ABC, alpha, beta, and gamma are in a ratio of 1:2:3. The longest side of the AB triangle is 30 cm long. Calculate the perimeter of the triangle CBS if S is the center of the side AB.
The interior angles of the triangle ABC, alpha, beta, and gamma are in a ratio of 1:2:3. The longest side of the AB triangle is 30 cm long. Calculate the perimeter of the triangle CBS if S is the center of the side AB. - Parallelogram diagonals
 Find the area of a parallelogram if the diagonals u1 = 15 cm and u2 = 12 cm and the angle formed by them is 30 degrees.
Find the area of a parallelogram if the diagonals u1 = 15 cm and u2 = 12 cm and the angle formed by them is 30 degrees. - Viewing angle
 The observer sees a straight fence 60 m long at a viewing angle of 30°. It is 102 m away from one end of the enclosure. How far is the observer from the other end of the enclosure?
The observer sees a straight fence 60 m long at a viewing angle of 30°. It is 102 m away from one end of the enclosure. How far is the observer from the other end of the enclosure? - Observation tower
 The observation tower has a height of 105 m above sea level. The ship is aimed at a depth angle of 1° 49' from the tower. How far is the ship from the base of the tower?
The observation tower has a height of 105 m above sea level. The ship is aimed at a depth angle of 1° 49' from the tower. How far is the ship from the base of the tower? - Power line pole
 From point A, the power pole is visible at an angle of 18 degrees. From place B, which we reach if we go from place A 30m towards the pillar at an angle of 10 degrees. Find the height of the power pole.
From point A, the power pole is visible at an angle of 18 degrees. From place B, which we reach if we go from place A 30m towards the pillar at an angle of 10 degrees. Find the height of the power pole. - Raindrops
 The train runs at a speed of 14 m/s, and raindrops draw lines on the windows, forming an angle of 60 degrees with the horizontal. What speed do drops fall?
The train runs at a speed of 14 m/s, and raindrops draw lines on the windows, forming an angle of 60 degrees with the horizontal. What speed do drops fall? - Loonie
 Loonie has three wooden sticks measuring 17 inches, 21 inches, and 25 inches. He lays them down to form a triangle. Find the measure of the angle enclosed by 17 inches and 21 inches. (Express answers to the nearest hundredths) (using the law of cosines)
Loonie has three wooden sticks measuring 17 inches, 21 inches, and 25 inches. He lays them down to form a triangle. Find the measure of the angle enclosed by 17 inches and 21 inches. (Express answers to the nearest hundredths) (using the law of cosines) - Calculate triangle
 In the triangle, ABC, calculate the sizes of all heights, angles, perimeters, and areas if given a=40cm, b=57cm, and c=59cm.
In the triangle, ABC, calculate the sizes of all heights, angles, perimeters, and areas if given a=40cm, b=57cm, and c=59cm. - Magnitude 25411
 There is a circle with a radius of 10 cm and its chord, which is 12 cm long. Calculate the magnitude of the central angle that belongs to this chord.
There is a circle with a radius of 10 cm and its chord, which is 12 cm long. Calculate the magnitude of the central angle that belongs to this chord. - The pond
 We can see the pond at an angle of 65°37'. Its endpoints are 155 m and 177 m away from the observer. What is the width of the pond?
We can see the pond at an angle of 65°37'. Its endpoints are 155 m and 177 m away from the observer. What is the width of the pond? - Maggie
 Maggie observes a car and a tree from a window. The angle of depression of the car is 45 degrees, and that of the tree is 30 degrees. If the distance between the vehicle and the tree is 100 m, find Maggie's distance from the tree.
Maggie observes a car and a tree from a window. The angle of depression of the car is 45 degrees, and that of the tree is 30 degrees. If the distance between the vehicle and the tree is 100 m, find Maggie's distance from the tree. - A trapezoid
 A trapezoid with a base length of a = 36.6 cm, with angles α = 60°, β = 48°, and the height of the trapezoid is 20 cm. Calculate the lengths of the other sides of the trapezoid.
A trapezoid with a base length of a = 36.6 cm, with angles α = 60°, β = 48°, and the height of the trapezoid is 20 cm. Calculate the lengths of the other sides of the trapezoid. - Cable car 2
 The cable car rises at an angle of 16° and connects the upper and lower station with an altitude difference of 1082 m. How long is the cable car's track?
The cable car rises at an angle of 16° and connects the upper and lower station with an altitude difference of 1082 m. How long is the cable car's track?
Do you have homework that you need help solving? Ask a question, and we will try to solve it. Solving math problems.
