Úloha roka
Stanovte počet prirodzených čísel od 1 do 106, ktoré končia štvorčíslím 2007.
Správna odpoveď:
Tipy na súvisiace online kalkulačky
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
kombinatorikaÚroveň náročnosti úlohy
Súvisiace a podobné príklady:
- Najviac deliteľov
Spomedzi prirodzených čísel od 1 do 100 nájdi to, ktoré má najviac deliteľov. - Prirodzených 7866
Nájdite súčet všetkých prirodzených čísel od 1 do 100, ktoré sú deliteľné 2 alebo 5 - Počet čísel
Nájdi počet všetkých trojciferných prirodzených čísel, ktoré sa dajú zostaviť z číslic 1,2,3,4 a pre ktoré platia súčasne ešte tieto podmienky: na mieste jednotiek je jedna z číslic 1,3,4, na mieste stoviek číslica 4 alebo 2. - Kolko 125
Kolko je trojciferných prirodzených čísel, ktoré môžeme utvoriť z cifier 0, 1, 2, ak sa v týchto číslach môžu cifry opakovať? - Cifry 4
Koľko je prirodzených čísel n väčších ako 4000, ktoré sú utvorené z cifier 0,1,3,7,9 pričom sa cifry neopakujú , b) Ako sa zmení počet prirodzených čísel tak, aby boli menšie ako 4000 a cifry sa môžu opakovať ? - PC nad 200
Určte počet všetkých prirodzených čísel väčších než 200, v ktorých sa vyskytujú cifry 1, 2, 4, 6, 8, a to každá najviac raz. - Súčet mocnín
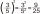Aký je súčet všetkých prirodzených čísel menších ako 100, ktoré sú mocninou čísla 4?
