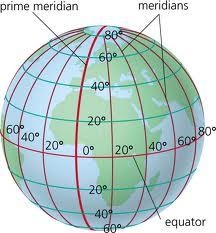
Rovnobežka
Vypočítaj dĺžku rovnobežky 48 stupňov a 10 minút.
Správna odpoveď:
Tipy na súvisiace online kalkulačky
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Vyskúšajte si prevody jednotiek uhlov uhlové stupne, minúty, sekundy, radiány.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Vyskúšajte si prevody jednotiek uhlov uhlové stupne, minúty, sekundy, radiány.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
stereometriaplanimetriagoniometria a trigonometriaJednotky fyzikálnych veličínÚroveň náročnosti úlohy
Odporúčame k tejto úlohe z matematiky si pozrieť toto výukové video: video1
Súvisiace a podobné príklady:
- Vypočítaj 448
 Vypočítaj povrch a objem pravidelného štvorbokého ihlana, ktorého hrana podstavy má dlžku 5 cm a ktorého výška je 10cm.
Vypočítaj povrch a objem pravidelného štvorbokého ihlana, ktorého hrana podstavy má dlžku 5 cm a ktorého výška je 10cm. - Štvorec 26
 Vypočítaj dlžku strany štvorca v cm, ktorého obsah je 48 cm štvorcových.
Vypočítaj dlžku strany štvorca v cm, ktorého obsah je 48 cm štvorcových. - Vypočítaj 84
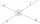 Vypočítaj veľkosť uhla BVC, ak pre veľkosti uhlov platí: AVB=37°48minut, CVD=52°30minut, AVD=118°
Vypočítaj veľkosť uhla BVC, ak pre veľkosti uhlov platí: AVB=37°48minut, CVD=52°30minut, AVD=118° - Rovnobežka
 Polomer Zeme je 6372 km dlhý. Vypočítajte dĺžku rovnobežky, ktorá má zemepisnú šírku 55°.
Polomer Zeme je 6372 km dlhý. Vypočítajte dĺžku rovnobežky, ktorá má zemepisnú šírku 55°. - Vypočítaj oblúk
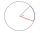 Vypočítaj dĺžku kružnicového oblúka a obsah kruhového výseku, ak polomer kruhu je 8,3 centimetrov a stredový uhol alfa=104 stupňov.
Vypočítaj dĺžku kružnicového oblúka a obsah kruhového výseku, ak polomer kruhu je 8,3 centimetrov a stredový uhol alfa=104 stupňov. - Rovnoramenný lichobežník RR
 V rovnoramennom lichobežníku ABCD vypočítaj chýbajúcu dĺžku strany "a" a potom jeho obsah. Strana b = d = 50 cm, c = 20 cm, výška = 48 cm.
V rovnoramennom lichobežníku ABCD vypočítaj chýbajúcu dĺžku strany "a" a potom jeho obsah. Strana b = d = 50 cm, c = 20 cm, výška = 48 cm. - Stredné priečky 2
 Vypočítaj dĺžku stredných priečok v rovnoramennom trojuholníku, ak dĺžka ramena je 52mm a výška na základnú má 48mm
Vypočítaj dĺžku stredných priečok v rovnoramennom trojuholníku, ak dĺžka ramena je 52mm a výška na základnú má 48mm
