Príklady na obsah rovinných útvarov - strana 73 z 131
Počet nájdených príkladov: 2606
- Dve lúky
 Kosci mali pokosiť dve lúky, z ktorých bola jedna dvakrát tak veľká ako druhá. V prvej polovici dňa sa rodelili na dve rovnaké skupiny. Jedna pokračovala v kosení vačšej lúky a do konca dňa ju celú pokosila. Druhá skupina kosila menšiu lúku, ale do konca
Kosci mali pokosiť dve lúky, z ktorých bola jedna dvakrát tak veľká ako druhá. V prvej polovici dňa sa rodelili na dve rovnaké skupiny. Jedna pokračovala v kosení vačšej lúky a do konca dňa ju celú pokosila. Druhá skupina kosila menšiu lúku, ale do konca - Vpísaná kružnica
 Do pravouhlého trojuholníka XYZ s pravým uhlom pri vrchole X je vpísaná kružnica s polomerom 5 cm. Určte obsah trojuholníka XYZ ak XZ=14cm.
Do pravouhlého trojuholníka XYZ s pravým uhlom pri vrchole X je vpísaná kružnica s polomerom 5 cm. Určte obsah trojuholníka XYZ ak XZ=14cm. - Opísaná kružnica
 Vypočítajte polomer kružnice opísaneho trojuholníku, ktorý má rozmery strán 8, 10 a 14cm.
Vypočítajte polomer kružnice opísaneho trojuholníku, ktorý má rozmery strán 8, 10 a 14cm. - Pan Liška
 Pan Liška sa rozhodol vymenit podlahy v niektorych miestnostiach svojho bytu. a) Kuchyňa je obdĺžnik so stranami 180 cm a 420cm. Koľko štvorcových dlaždíc so stranou dlhou 20 cm bude potrebovať? b) Koľko balíčkov s dlazdicami musi kupiť, ak v jednom balíč
Pan Liška sa rozhodol vymenit podlahy v niektorych miestnostiach svojho bytu. a) Kuchyňa je obdĺžnik so stranami 180 cm a 420cm. Koľko štvorcových dlaždíc so stranou dlhou 20 cm bude potrebovať? b) Koľko balíčkov s dlazdicami musi kupiť, ak v jednom balíč - Na obrázku 5
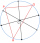 Na obrázku sú znázornené tri obce A, B, C a ich vzájomné vzdušné vzdialenosti. Nová priamočiara želežničná trať má byť postavená tak, aby zo všetkých obcí bolo k trati rovnako ďaleko a aby táto vzdialenosť bola najmenšia možná. Ako ďaleko budú od trate? a
Na obrázku sú znázornené tri obce A, B, C a ich vzájomné vzdušné vzdialenosti. Nová priamočiara želežničná trať má byť postavená tak, aby zo všetkých obcí bolo k trati rovnako ďaleko a aby táto vzdialenosť bola najmenšia možná. Ako ďaleko budú od trate? a - Záhradka 7
 Záhradka tvaru lichobežníka má základne dĺžky 44 m a 16 m, ich vzdialenosť je 25 m. Koľko štvorcových metrov jej výmery zostane na výsadbu stromov, ak 1/5 celej plochy bude využitá na stavbu chaty, vybudovanie dvorčeka a cesty. Dá sa z daných údajov zisti
Záhradka tvaru lichobežníka má základne dĺžky 44 m a 16 m, ich vzdialenosť je 25 m. Koľko štvorcových metrov jej výmery zostane na výsadbu stromov, ak 1/5 celej plochy bude využitá na stavbu chaty, vybudovanie dvorčeka a cesty. Dá sa z daných údajov zisti - Zubár
 Lekár zdvíha kreslo s pacientom pomocou hydraulického zariadenia . Obsah menšieho piesta je 5 cm². Obsah väčšieho piesta je 200 cm². Hmotnosť kresla je 30 kg, hmotnosť pacienta 100kg. Zdvihne lekár silou 20 N kreslo s pacientom do vhodnej výšky pre svoju
Lekár zdvíha kreslo s pacientom pomocou hydraulického zariadenia . Obsah menšieho piesta je 5 cm². Obsah väčšieho piesta je 200 cm². Hmotnosť kresla je 30 kg, hmotnosť pacienta 100kg. Zdvihne lekár silou 20 N kreslo s pacientom do vhodnej výšky pre svoju - Pozemok 14
 Pozemok, ktorý má rozmery 220 m a 308 m, chce majiteľ rozdeliť na rovnako veľké štvorcové parcely s čo najväčšou výmerou. Aká dlhá bude jedna strana parcely?
Pozemok, ktorý má rozmery 220 m a 308 m, chce majiteľ rozdeliť na rovnako veľké štvorcové parcely s čo najväčšou výmerou. Aká dlhá bude jedna strana parcely? - Vpísaný štvorec
 Je daná kružnica, do ktorej je vpísaný štvorec. Menší štvorec je vpísaný do kruhovej úseče tvorenej stranou štvorca a oblúkom danej kružnice. Aký je pomer plôch veľkého a malého štvorca?
Je daná kružnica, do ktorej je vpísaný štvorec. Menší štvorec je vpísaný do kruhovej úseče tvorenej stranou štvorca a oblúkom danej kružnice. Aký je pomer plôch veľkého a malého štvorca? - Štvorlístok
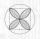 Vypočítajte obsah štvorlístka, ktorý je vpísaný do štvorca, ktorého strana má dĺžku 6 cm.
Vypočítajte obsah štvorlístka, ktorý je vpísaný do štvorca, ktorého strana má dĺžku 6 cm. - Coulombov zákon
 Tri rovnaké kladné náboje Q sú umiestnené vo vrcholoch rovnoramenného pravouhlého trojuholníka ABC. Pravý uhol je pri vrchole A. Dĺžka strany AB je 1 m. Aká je intenzita elektrického poľa v strede S strany BC, t. j. aká sila by pôsobila na kladný náboj q
Tri rovnaké kladné náboje Q sú umiestnené vo vrcholoch rovnoramenného pravouhlého trojuholníka ABC. Pravý uhol je pri vrchole A. Dĺžka strany AB je 1 m. Aká je intenzita elektrického poľa v strede S strany BC, t. j. aká sila by pôsobila na kladný náboj q - Záhadný obsah
 Je daný lichobežník ABCD. Vypočítaj jeho obsah, ak plocha trojuholníka DBC je 27 cm².
Je daný lichobežník ABCD. Vypočítaj jeho obsah, ak plocha trojuholníka DBC je 27 cm². - Dvaja 22
 Dvaja kamaráti Mário a Jano bývali bývali na dvoch rôznych stranách diaľnice. Rozhodli sa, že zistia, aká je široká. Mário nakreslil obrázok, na základe ktorého potom na druhý deň uskutočnili meranie Namerali hodnoty a =5m, b= 5,9 m, d = 5 m. Vypočitajte
Dvaja kamaráti Mário a Jano bývali bývali na dvoch rôznych stranách diaľnice. Rozhodli sa, že zistia, aká je široká. Mário nakreslil obrázok, na základe ktorého potom na druhý deň uskutočnili meranie Namerali hodnoty a =5m, b= 5,9 m, d = 5 m. Vypočitajte - Traja výletníci
 Aleš, Karol a Simon sa vypravili na výlet o 6,45. Do cieľa dorazili o 9,15. Niesli so sebou jeden batoh a striedali sa oň po 20 minútach. Prvý úsek ho niesol Karol, o 8,30 zase Simon. a) Kto niesol batoh druhý úsek? b) Koľko minút ho niesol Aleš, koľko Ka
Aleš, Karol a Simon sa vypravili na výlet o 6,45. Do cieľa dorazili o 9,15. Niesli so sebou jeden batoh a striedali sa oň po 20 minútach. Prvý úsek ho niesol Karol, o 8,30 zase Simon. a) Kto niesol batoh druhý úsek? b) Koľko minút ho niesol Aleš, koľko Ka - Čokoládova roláda
 Kocka čokoládovej rolády s hranou 5 cm váži 30g. Koľko kalórií v sebe bude obsahovať tá istá čokoládová roláda tvare hranola s dĺžkou 0,5 m, ktorej prierez je rovnoramenný lichobežník so základňami 25 a 13 cm a ramenami 10 cm. Viete, že v 100 g tejto rolá
Kocka čokoládovej rolády s hranou 5 cm váži 30g. Koľko kalórií v sebe bude obsahovať tá istá čokoládová roláda tvare hranola s dĺžkou 0,5 m, ktorej prierez je rovnoramenný lichobežník so základňami 25 a 13 cm a ramenami 10 cm. Viete, že v 100 g tejto rolá - Myši vyhlodali
 Myši vyhlodali do plátku syra kruhové diery. Syr má tvar kruhivého výseku s polomerom 20 cm a uhlom 90 stupňov. Akú časť syra v percentách myši zožrali, ak vyhlodali 20 dier s priemerom 2 cm?
Myši vyhlodali do plátku syra kruhové diery. Syr má tvar kruhivého výseku s polomerom 20 cm a uhlom 90 stupňov. Akú časť syra v percentách myši zožrali, ak vyhlodali 20 dier s priemerom 2 cm? - Rozkladací stôl
 Rozkladací kuchynský stôl má v bežnej podobe tvar obdĺžnika s obsahom 168dm² (strana a je dlhá 14 dm) . V prípade potreby sa môže zväčšiť vysunutím dvoch dosiek v tvare polkruhov (pri stranách b). O koľko percent sa takto zväčší plocha stola? Výsledok tre
Rozkladací kuchynský stôl má v bežnej podobe tvar obdĺžnika s obsahom 168dm² (strana a je dlhá 14 dm) . V prípade potreby sa môže zväčšiť vysunutím dvoch dosiek v tvare polkruhov (pri stranách b). O koľko percent sa takto zväčší plocha stola? Výsledok tre - Parabolický úsek
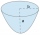 Parabolický úsek má základňu a = 4 cm a výšku v = 6 cm. Vypočítajte objem telesa, ktoré vznikne rotáciou tejto úseče a) okolo svojej základne b) okolo svojej osi. Vopred ďakujem za riešenie.
Parabolický úsek má základňu a = 4 cm a výšku v = 6 cm. Vypočítajte objem telesa, ktoré vznikne rotáciou tejto úseče a) okolo svojej základne b) okolo svojej osi. Vopred ďakujem za riešenie. - MO Z8–I–6 2018
 V lichobežníku KLMN má základňa KL veľkosť 40 cm a základňa MN má velkosť 16 cm. Bod P leží na úsečke KL tak, že úsečka NP rozdeľuje lichobežník na dve časti s rovnakými obsahmi. Určte veľkosť úsečky KP.
V lichobežníku KLMN má základňa KL veľkosť 40 cm a základňa MN má velkosť 16 cm. Bod P leží na úsečke KL tak, že úsečka NP rozdeľuje lichobežník na dve časti s rovnakými obsahmi. Určte veľkosť úsečky KP. - Vystrihol som obdĺžniky
 Vystrihol som si dva obdĺžniky s obsahmi 54 cm², 90 cm². Ich strany sú vyjadrene celými číslami v centimetroch. Ak tieto obdĺžniky priložím k sebe, dostanem obdĺžnik s obsahom 144 cm². Aké rozmery môže mat tento veľký obdĺžnik? Napíš všetky možnosti. Svoj
Vystrihol som si dva obdĺžniky s obsahmi 54 cm², 90 cm². Ich strany sú vyjadrene celými číslami v centimetroch. Ak tieto obdĺžniky priložím k sebe, dostanem obdĺžnik s obsahom 144 cm². Aké rozmery môže mat tento veľký obdĺžnik? Napíš všetky možnosti. Svoj
Máš príklad, ktorý si tu nenašiel vyriešenú? Pošli nám príklad a my Ti ho skúsime vypočítať.
