Dva válce
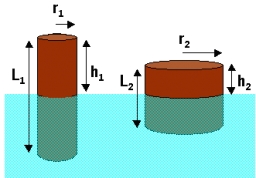
Obdélník o rozměrech 8 cm a 4 cm otočíme o 360º nejprve kolem delší strany, čímž vznikne první těleso. Potom obdélník podobně otočíme kolem kratší strany, čímž vznikne druhé těleso. Určete poměr povrchů prvního a druhého tělesa.
Vaše odpověď:
Vaše odpověď:
Tipy na související online kalkulačky
Vyzkoušejte naši kalkulačka na přepočet poměru.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
algebraaritmetikastereometrieplanimetriezákladní operace a pojmyJednotky fyzikálních veličinÚroveň náročnosti úkolu
Související a podobné příklady:
- Obdélník - strany
Jaký je obvod obdélníku, jehož obsah je 456 cm² a délka kratší strany je o 26 cm kratší než délka delší strany? - Strany obdélníku
Rozměry obdélníku jsou v poměru 4:12. Pokud je kratší strana 12 cm, jaká je délka delší strany v centimetrech? - Délka kratší strany hřiště
Hřiště má tvar obdélníku. Délka čáry po jeho obvodu je 440 m. Delší strana hřiště má délku 140 m. Kolik metrů měří délka kratší strany hřiště? - Dvě tělesa
Dvě tělesa, jejichž počáteční vzdálenost je 240 m, se pohybují rovnoměrně zrychleně proti sobě. První těleso má počáteční rychlost 4 m/s a zrychlení 3 m/s², druhé těleso má počáteční rychlost 6 m/s a zrychlení 2 m/s². Určete dobu, za kterou dojde ke koliz - Strany 14
Strany lesního obdélníkového pozemku jsou v poměru 11:7. Kratší strana pozemku má délku 175 metrů. Vypočítejte delší stranu obdélníkového pozemku. Kolik kroků bychom udělali, kdybychom celý pozemek obešli? Délka 1 kroku je průměrně 60 cm. - Délka strany a obvod pozemků
Pozemek tvaru obdélníku má strany dlouhé 20 m a 28 m. Vypočítej obsah pozemku a zjisti, jak dlouhá musí být delší strana pozemku se stejným obsahem, pokud kratší strana bude dlouhá 16 metrů. Vypočítej i délku plotu kolem každého pozemku - Kosodélník
Kosodélník (rovnoběžník) má delší stranu dlouhou 50 cm. Velikost jeho jedné výšky je 4krát větší než velikost jeho druhé výšky. Vypočítejte v centimetrech délku kratší strany tohoto rovnoběžníku.
