Otočíme o 360º
Obdĺžnik s rozmermi 8 cm a 4 cm otočíme o 360º najprv okolo dlhšej strany, čím vznikne prvé teleso. Potom obdĺžnik podobne otočíme okolo kratšej strany, čím vznikne druhé teleso. Určte pomer povrchov prvého a druhého telesa.
Vaša odpoveď:
Vaša odpoveď:
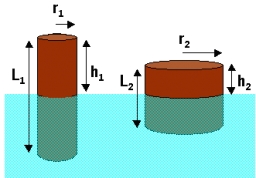
Tipy na súvisiace online kalkulačky
Vyskúšajte našu kalkulačka na prepočet pomeru.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
algebraaritmetikastereometriaplanimetriazákladné operácie a pojmyJednotky fyzikálnych veličínÚroveň náročnosti úlohy
Súvisiace a podobné príklady:
- Obĺžnik - strany
Aký je obvod obdĺžnika, ktorého obsah je 850 cm² a dĺžka kratšej strany je o 9 cm kratšia ako dĺžka dlhšej strany? - Dve telesá
Dve telesá, ktorých počiatočná vzdialenosť je 240 m, sa pohybujú rovnomerne zrýchlene proti sebe. Prvé teleso má začiatočnú rýchlosti 4 m/s a zrýchlenie 3 m/s², druhé teleso má začiatočnú rýchlosť 6 m/s a zrýchlenie 2 m/s². Určte dobu, za ktorú dôjde ku k - Teleso 6
Vypočítaj objem a povrch telesa, ktoré vznikne tak, že z kvádra s rozmermi 10 cm 15 cm a 20 cm vyrežeme trojboký hranol s rovnakou výškou, ktorého podstava je pravouhlý trojuhoľnik s rozmermi 3 cm , 4 cm a 5 cm - Rotácia
Vypočítaj povrch a objem kužeľa, ktorý vznikne rotáciou pravouhlého trojuholníka ABC s odvesnami dlhými 6 cm a 9 cm okolo kratšej odvesny. - Dve telesá 2
Dve telesá sa pohybujú rovnakým smerom rovnomerne priamočiaro, rýchlosťami 5 cm/s a 10 cm/s. Pohyb prvého telesa začal o 2 s skôr než pohyb druhého telesa, z bodu nachádzajúceho sa vo vzdialenosti 20 cm od začiatočného bodu (kde sa nachádzalo druhé teleso - Obvod 37
Obvod prvého kolesa je o 0,5 m väčší ako obvod druhého kolesa. Prvé koleso sa na dráhe 36 m otočí toľkokrát, ako druhé koleso na dráhe 30 m. Urč obvody oboch kolies. - Urči súčet
Urči súčet troch čísel, ak prvé číslo je 328, druhé je o 28 menšie a tretie predstavuje ¼ prvého čísla.
