Úhly
Pro velikost úhlů trojúhelníku platí x: y = 7:5 a úhel z je o 42 ° menší než úhel y. Urč velikosti úhlů x, y, z.
Vaše odpověď:
Vaše odpověď:
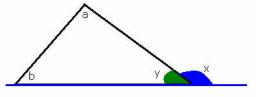
Tipy na související online kalkulačky
Vyzkoušejte naši kalkulačka na přepočet poměru.
Máte lineární rovnici nebo soustavu rovnic a hledáte její řešení? Nebo máte kvadratickou rovnici?
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Máte lineární rovnici nebo soustavu rovnic a hledáte její řešení? Nebo máte kvadratickou rovnici?
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
algebraplanimetriezákladní operace a pojmyJednotky fyzikálních veličinÚroveň náročnosti úkolu
Související a podobné příklady:
- Jsou podobné
Trojúhelníky ABC a A'B'C 'jsou podobné s koeficientem podobnosti 2. Velikosti úhlů trojúhelníku ABC jsou alfa = 35°, beta = 48°. Urči velikosti všech úhlů trojúhelníku A'B'C '. - Koeficient podobnosti
Trojúhelníky ABC a A "B" C "jsou podobné koeficientem podobnosti 2. Velikosti úhlů trojúhelníku ABC jsou α = 35° a β = 48°. Urči velikosti všech úhlů trojúhelníku A" B "C". - Velikost úhlu BVC
Vypočítej velikost úhlu BVC, pokud pro velikosti úhlů platí: AVB=37°48minut, CVD=52°30minut, AVD=118° - Pro velikosti
Pro velikosti vnitřních úhlů čtyřúhelníku ABCD platí: úhel alfa je o 26° větší než úhel beta, dvojnásobek úhlu Beta je o 5° menší než úhel gama a úhel gama je o 36° větší než úhel delta. Určete úhly. - V pravoúhlém 6
V pravoúhlém trojúhelníku je jeden ostrý úhel o 20° menší než druhý ostrý úhel. Urči velikost vnitřních úhlů v trojúhelníku. - Trojúhelník XYZ
Pro trojúhelník XYZ platí, že ∠X = (6 g + 14)° a vnější úhel k ∠X měří (5 g + 45)°. Najděte velikost úhlu ∠X a její vnější úhel. - Úhly vnitřné
Jeden vnitřní úhel trojúhelníku JAR má velikost 25 °. Rozdíl velikosti zbývajících dvou je 15°. Urč velikost těchto úhlů.
