Pan Cuketa
Pan Cuketa měl obdelníkovou zahradu. jejíž obvod byl 28 metrů. Obsah celé zahrady vyplnily právě čtyři čtvercové záhony, jejichž rozměry v metrech byly vyjádřeny celými čísly. Určete, jaké rozměry mohla mít zahrada. najděte všechny možnosti a zapište n jako počet řešení.
Správná odpověď:
Zobrazuji 2 komentáře:
Mo-radca
Nápověda. Uvědomte si, že čtverce nemusí mít stejné rozměry.
Možné řešení. Obvod 28 = 2 · 14 metrů lze pomocí kladných celých čísel vyjádřit pouze několika málo způsoby. Postupně všechny probereme a zjistíme, zda lze odpovídající záhon rozdělit na čtyři čtverce s celočíselnými rozměry:
• 28 = 2 · (13 + 1), v takovém případě potřebujeme 13 čtverců
• 28 = 2 · (12 + 2), v takovém případě potřebujeme nejméně 6 čtverců
• 28 = 2 · (11 + 3), v takovém případě potřebujeme nejméně 6 čtverců
• 28 = 2 · (10 + 4), v takovém případě stačí 4 čtverce
• 28 = 2 · (9 + 5), v takovém případě potřebujeme nejméně 6 čtverců
• 28 = 2 · (8 + 6), v takovém případě stačí 4 čtverce
• 28 = 2 · (7 + 7), v takovém případě by byl záhon čtvercový a ne obdélníkový.
Zahrada mohla mít rozměry 10 × 4 nebo 8 × 6 metrů.
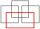
Jiné řešení. Uvažujme, jak lze složit jeden obdélník ze čtyř čtverců (obecně různých celočíselných rozměrů). To lze udělat pouze následujícími způsoby:
Pokud velikost strany nejmenšího čtverce v metrech označíme a, potom obvod obdélníku v jednotlivých případech je:
• 2 · (4a + a) = 10a, což není rovno 28 pro žádné celé a.
• 2 ·(5a + 2a) = 14a, což je rovno 28, právě když a = 2; obdélník má v takovém případě rozměry 10 × 4 metrů.
• 2 · (5a + 3a) = 16a, což není rovno 28 pro žádné celé a.
• 2 ·(4a + 3a) = 14a, což je rovno 28, právě když a = 2; obdélník má v takovém případě rozměry 8 × 6 metrů.
Možné řešení. Obvod 28 = 2 · 14 metrů lze pomocí kladných celých čísel vyjádřit pouze několika málo způsoby. Postupně všechny probereme a zjistíme, zda lze odpovídající záhon rozdělit na čtyři čtverce s celočíselnými rozměry:
• 28 = 2 · (13 + 1), v takovém případě potřebujeme 13 čtverců
• 28 = 2 · (12 + 2), v takovém případě potřebujeme nejméně 6 čtverců
• 28 = 2 · (11 + 3), v takovém případě potřebujeme nejméně 6 čtverců
• 28 = 2 · (10 + 4), v takovém případě stačí 4 čtverce
• 28 = 2 · (9 + 5), v takovém případě potřebujeme nejméně 6 čtverců
• 28 = 2 · (8 + 6), v takovém případě stačí 4 čtverce
• 28 = 2 · (7 + 7), v takovém případě by byl záhon čtvercový a ne obdélníkový.
Zahrada mohla mít rozměry 10 × 4 nebo 8 × 6 metrů.
Jiné řešení. Uvažujme, jak lze složit jeden obdélník ze čtyř čtverců (obecně různých celočíselných rozměrů). To lze udělat pouze následujícími způsoby:
Pokud velikost strany nejmenšího čtverce v metrech označíme a, potom obvod obdélníku v jednotlivých případech je:
• 2 · (4a + a) = 10a, což není rovno 28 pro žádné celé a.
• 2 ·(5a + 2a) = 14a, což je rovno 28, právě když a = 2; obdélník má v takovém případě rozměry 10 × 4 metrů.
• 2 · (5a + 3a) = 16a, což není rovno 28 pro žádné celé a.
• 2 ·(4a + 3a) = 14a, což je rovno 28, právě když a = 2; obdélník má v takovém případě rozměry 8 × 6 metrů.
7 let 4 Likes
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
Téma:
Úroveň náročnosti úkolu:
Doporučujeme k tomuto príkladu si prohlédnout toto výukové video: video1
Související a podobné příklady:
- Čtverečních 31761
Pan Marek si chce v zahradě vybudovat kruhové jezírko. Jeho přáním je, aby obvod jezírka v metrech i rozloha v metrech čtverečních byly vyjádřeny stejnými čísly. Jaký poloměr má mít jezírko? - Obdélník
Obvod obdélníku je 22 cm a obsah 30 cm². Určete jeho rozměry, jsou-li délky stran obdélníku v centimetrech vyjádřeny celými čísly. - Obdélníky
Vystřihl jsem si dva obdélníky s obsahy 54 cm², 90 cm². Jejich strany jsou vyjádřené celými čísly v centimetrech. Pokud tyto obdélníky přiložím k sobě, dostanu obdélník s obsahem 144 cm². Jaké rozměry může mít tento velký obdélník? Napiš všechny možnosti. - Obvod záhrady
Obvod obdélníkové zahrady Hruškových je 98 metrů. Šířka zahrady je právě o 60% kratší než její délka. Určete v metrech rozměry obdélníkové zahrady. Určete v metrech čtverečních výměru zahrady. - Obdélníkové 8136
Rozdělte čtvercovou zahradu s obvodem 124 m na dvě obdélníkové zahrady tak, aby plot jedné zahrady byl o 10 m delší než plot druhé zahrady. Jaké rozměry budou mít tyto obdélníkové zahrady? - Zahrada
Zahrada má tvar čtverce o = 124m, udělej dvě obdélníkové zahrady aby jedna zahrada měla obvod o 10m více než druhá. Jaké rozměry budou mít zahrady? - Obdélník
Zahrada má tvar obdélníku a má obvod délky 130 a obsah 800,25 m². Vypočtěte rozměry zahrady. - Obdélníkovou 3175
Chceme ohradit obdélníkovou zahradu, jejíž poměr délky a šířky je 2:1 a jejíž polovina obvodu hraničí s cestou. Cesta ohrazení podél cesty stojí 7 eur za metr ostatní ohrazení jen 3 eura za metr. Kolik arů má zahrada, pokud její ohrazení stojí 363 eur. - Zahrada
Zahrada má tvar pravoúhlého lichoběžníku, jehož základny mají rozměry 60 m a 30 m a kolmé rameno 40 m. Majitel tuto zahradu vyměnil za Rovnoběžníkový, jejíž obsah je 7/9 obsahu lichoběžníkové zahrady. Jakou výměru v arech má nová zahrada? - C–I–4 MO 2017
Určete největší celé číslo n, při kterém lze čtvercovou tabulku n×n zaplnit přirozenými čísly od 1 do n² (n na druhou) tak, aby v každé její čtvercové části 3×3 byla zapsána aspoň jedna druhá mocnina celého čísla. - Kroky
Abychom obešli zahradu musíme udělat 144 kroků. Na šířku o 8 kroků méně než na délku. Jeden krok je dlouhý 5 decimetrů. Jaké jsou rozměry zahrady? Jaký je její obvod a obsah? - Zahrada 82159
Zahrada tvaru čtverce má ze tří stran živý plot. Jeho délka je 36 metrů. Jaký je obsah zahrady v m²? - Přirozenými 70304
Kolik obdélníků, jejichž délky stran jsou vyjádřeny přirozenými čísly, má obsah 96 cm²? - Zajímava vlastnost
Pozemek tvaru obdélníka má tu zajímavou vlastnost, že obvod v metrech a obsah v metrech čtverečných jsou stejná čísla. Jaké rozměry může obdélník mít? - Záhrada
Zahrada kolem nového Majera je rozdělena takto: 35% zeleninové záhony, 30% ovocný sad, 10% květiny a zbytek 120 m² je trávník. Jaká je celková výměra zahrady? - Zahrada 24
Čtvercová zahrada má obsah 735 m² a je celá oplocená. Vypočítejte délku strany zahrady a délku jejího plotu. - Obdélníky Kolik je obdélníků, jejichž délky stran jsou vyjádřeny přirozenými čísly a mají obsah 1572 cm²?
