Pán Cuketa

Ťahák: Uvedomte si, že štvorce nemusia mať rovnaké rozmery.

Možné riešenie. Obvod 28 = 2 · 14 metrov možno pomocou kladných celých čísel vyjadriť len niekoľko málo spôsobmi. Postupne všetky preberieme a zistíme, či možno zodpovedajúce záhon rozdeliť na štyri štvorce s celočíselnými rozmermi:

• 28 = 2 · (13 + 1), v takom prípade potrebujeme 13 štvorcov
• 28 = 2 · (12 + 2), v takom prípade potrebujeme najmenej 6 štvorcov
• 28 = 2 · (11 + 3), v takom prípade potrebujeme najmenej 6 štvorcov
• 28 = 2 · (10 + 4), v takom prípade stačí 4 štvorce
• 28 = 2 · (9 + 5), v takom prípade potrebujeme najmenej 6 štvorcov
• 28 = 2 · (8 + 6), v takom prípade stačí 4 štvorce
• 28 = 2 · (7 + 7), v takom prípade by bol záhon štvorcový a nie obdĺžnikový.

Záhrada mohla mať rozmery 10 × 4 alebo 8 × 6 metrov.

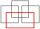
Iné riešenie. Uvažujme, ako možno zložiť jeden obdĺžnik zo štyroch štvorcov (všeobecne rôznych celočíselných rozmerov). To možno urobiť iba nasledujúcimi spôsobmi:

Ak veľkosť strany najmenšieho štvorca v metroch označíme a, potom obvod obdĺžnika v jednotlivých prípadoch je:

• 2 · (4a + a) = 10a, čo nie je presne 28 pre žiadne celé a.
• 2 · (5a + 2a) = 14a, čo je presne 28, práve keď a = 2; obdĺžnik má v takom prípade rozmery 10 × 4 metrov.
• 2 · (5a + 3a) = 16a, čo nie je presne 28 pre žiadne celé a.
• 2 · (4a + 3a) = 14a, čo je presne 28, práve keď a = 2; obdĺžnik má v takom prípade rozmery 8 × 6 metrov.

Mohli by ste mi to prosim vysvetlit niak tak jednoduchsie?

A celkovo napisat ten postup prosim ? Ja tomu nerozumiem :(

Ahoj Hana; no v prípade MO sa nejedná o ľahké príklady, ktorým musí rozumieť každý.  Ale tým že toto riešenie (vlastne dve) budeš študovať možno aj týždne,  sa niečo nové naučíš...

Tak dakujem este sa to pokusim pochopit :)