Povrch pláště , objem

V rotačním válci je dáno: povrch pláště (bez podstav) S = 96 cm2 a objem V = 192 cm krychlových. Vypočítejte poloměr a výšku tohoto válce.

Správná odpověď:

r =  4 cm
h =  3,8197 cm

Postup správného řešení:

S=96 cm2 V=192 cm3  S = 2π⋅ r⋅ h V = π r2 h  h =  2π⋅ rS​  V = π r2  2π⋅ rS​  V =  2r⋅ S​  r=2⋅ V/S=2⋅ 192/96=4 cm  h=2π⋅ rS​=2⋅ 3,1416⋅ 496​≐3,8197 cm   Zkousˇka spraˊvnosti:  S1​=2π⋅ r⋅ h=2⋅ 3,1416⋅ 4⋅ 3,8197=96 V1​=π⋅ r2⋅ h=3,1416⋅ 42⋅ 3,8197=192  S1​=S, V1​=V

Zkusit jiný příklad


Našel jsi chybu či nepřesnost? Klidně nám ji napiš.







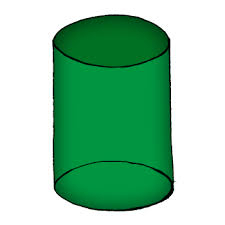
Tipy na související online kalkulačky
Hledáte pomoc s výpočtem kořenů kvadratické rovnice?
Máte lineární rovnici nebo soustavu rovnic a hledáte její řešení? Nebo máte kvadratickou rovnici?
Tip: Převody jednotky objemu vám pomůže naše kalkulačka pro převody jednotek objemu.

K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:

Jednotky fyzikálních veličin:

Úroveň náročnosti úkolu:

Související a podobné příklady: