Mnohočleny - trojčleny
Nalezněte všechny trojčleny
P(x)=a∗x2+b∗x+c
s celočíselnými koeficienty a, b a c, pro která platí
P(1) < P(2) < P(3)
a zároveň
((P(1)) 2 + ((P(2)) 2 + ((P(3)) 2 = 22.
Vaše odpověď:
P(x)=a∗x2+b∗x+c
s celočíselnými koeficienty a, b a c, pro která platí
P(1) < P(2) < P(3)
a zároveň
((P(1)) 2 + ((P(2)) 2 + ((P(3)) 2 = 22.
Vaše odpověď:
Tipy na související online kalkulačky
Hledáte pomoc s výpočtem kořenů kvadratické rovnice?
Řešíte Diofantovské problémy a hledáte kalkulačku diofantovských celočíselných rovnic?
Řešíte Diofantovské problémy a hledáte kalkulačku diofantovských celočíselných rovnic?
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
algebraaritmetikazákladní operace a pojmytémaÚroveň náročnosti úkolu
Související a podobné příklady:
- Soustava lineárních rovnic
Napiš soustavu 3 lineárních rovnic se 3 proměnnými (x. Y. z), která má všechny koeficienty nenulové a řešení x= 2+t, y=3-2t, z=t, kde t€R. To, že soustava má všechny koeficienty nenulové, znamená, že v rozšířené matici soustavy jsou všechna čísla nenulové - Součin a součet kořenů
Najděte součin a součet kořenů kvadratické rovnice x² + 3x - 9 = 0 Aplikujte vztahy mezi kořeny a koeficienty kvadratické rovnice. - Čtyřciferná čísla
Najděte všechna čtyřciferná čísla abcd, pro která platí: abcd = 20 . ab + 16 . cd, kde ab, cd jsou dvouciferné čísla z číslic a, b, c, d. - Kvadratické trojčleny
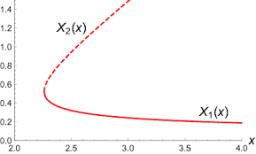
Pro každý z následujících problémů určete kořeny rovnice. Vzhledem k kořenům načrtněte graf a vysvětlete, jak se váš náčrt shoduje s danými kořeny a tvarem rovnice: g(x)=36x²-12x+5 h(x)=x²-4x+20 f(x)=4x²-24x+45 p(x)=9x²-36x+40 g(x)=x²-2x+10 g(x)=x2-x-6 - Kvadratická rovnice
Kvadratická rovnice -7x²+bx+c=0 má kořeny x1 = 53 a x2 = -34. Vypočítejte koeficienty b a c. - Určete dvojice
Určete všechny dvojice (m, n) přirozených čísel, pro něž platí m + s(n) = n + s(m) = 70, kde s(a) značí ciferný součet přirozeného čísla a. - Rovnice 39
Rovnice linearní funkcí je : y=-3x+4 a) urči průsečíky s osami načrtni graf b) pro které x platí f(x)=-1 c) pro které x platí f(x)=0 d) pro které y platí f(-1/2)=y
