Kyvadlo
Vypočítejte délku kyvadla, které v nejnižší poloze je o 2 cm nižší než při vychýlení v nejvyšší poloze. Délka kruhového oblouku, kterou popíše při pohybu je 20 cm.
Vaše odpověď:
Vaše odpověď:
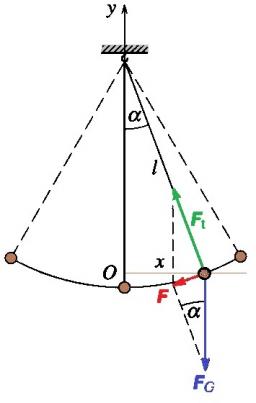
Tipy na související online kalkulačky
Chcete proměnit jednotku délky?
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
planimetrieJednotky fyzikálních veličinÚroveň náročnosti úkolu
Doporučujeme k tomuto príkladu si prohlédnout toto výukové video: video1
Související a podobné příklady:
- Kruhový oblouk
Vypočítejte délku kruhového oblouku, pokud průměr d = 20 cm a úhel alfa = 142° - Nejvyšší a nejnižší
Jenn je nejvyšší v týmu. Je 1 1/2krát vyšší než nejnižší dívka, která měří 4 1/4 stopy. Kolik měří Jebb? - Délka
Délka kružnice je 24 cm. Jaká je délka kruhového oblouku příslušejícího úhlu 30°? - Úseč
Vypočítejte plochu S úseče a délku kruhového oblouku l. Výška úseče je 2 cm a úhel α = 60°. Pomůcka: S = 1/2 r². (Β-sinβ) - Vypočítej 107
Vypočítej středový úhel a délku kruhového oblouku, je-li poloměr r = 21 cm a obsah výseče 328,5 cm². - Délka oblouku záhonu
Obvod kruhového záhonu je 36 m. Zjisti délku části jeho obvodu, která přísluší daným středovým úhlům 180° - Středový úhel
Vypočítej délku kružnicového oblouku a obsah kruhového výseku, pokud poloměr kruhu je 8,3 centimetrů a středový úhel alfa=104 stupňů.
