Z8 MO 2021

V dané skupině čísel je jedno číslo rovno průměru všech, největší číslo je o 7 větší než průměr, nejmenší je o 7 menší než průměr a většina čísel ze skupiny má podprůměrnou hodnotu.

Jaký nejmenší počet čísel může být ve skupině?

Správná odpověď:

n =  5

Postup správného řešení:

x1​ = 7 +μ x2​ = μ − 7 cnt( xi​ < μ ) ≥ n/2  μ =  nΣ xi​​  x2​ < μ x1​ > μ  n=2, μ = 0 n=3, x3​ = μ = 0  μ=1  x1​=μ+7=1+7=8 x2​=μ−7=1−7=−6 x3​=(μ⋅ 3−x1​−x2​)/1=(1⋅ 3−8−(−6))/1=1 μ3​=3x1​+x2​+x3​​=38+(−6)+1​=1  y1​=μ+7=1+7=8 y2​=μ−7=1−7=−6 y3​=(μ⋅ 4−y1​−y2​)/2−1=(1⋅ 4−8−(−6))/2−1=0 y4​=(μ⋅ 4−y1​−y2​−y3​)/1=(1⋅ 4−8−(−6)−0)/1=2 μ4​=4y1​+y2​+y3​+y4​​=48+(−6)+0+2​=1 cnt(y<μ) = 2 cnt(y≥μ) = 1+1  z1​=μ+7=1+7=8 z2​=μ−7=1−7=−6 z3​=(μ⋅ 5−z1​−z2​)/3−1=(1⋅ 5−8−(−6))/3−1=0 z4​=z3​=0 z5​=(μ⋅ 5−z1​−z2​−z3​−z4​)/1=(1⋅ 5−8−(−6)−0−0)/1=3 μ5​=5z1​+z2​+z3​+z4​+z5​​=58+(−6)+0+0+3​=1 cnt(z<μ) = 3 cnt(z≥μ) = 1+1  n=5

Zkusit jiný příklad


Našel jsi chybu či nepřesnost? Klidně nám ji napiš.



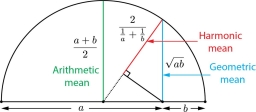
Zobrazuji 4 komentáře:
Danka
n = 5... mysleme si to proto, že ze zadání je jasné, že jedno číslo je už např. a druhé poprůměrně. Tj. průměr zbytku n-2 čísel musí být opět průměrem.

Při n=3 by to třetí číslo musela být nula.
Při n=4 by jedno ze dvou posledních čísel bylo podprůměrné a druhé nadprůměrné.
Teprve při n=5 mohou být voleny 3 čísla takto - dvě čísla podprůměrně (např od průměru o 1 menší) a jedno nadprůměrné (a bude o dvojnásobek vyšší než průměr než ty dvě menší, tj. o 2 vyšší než průměr).

3 roky  3 Likes
Ondra
Myslím si, že n=6, jelikož je v zadání jasně napsáno, že jedno číslo se musí rovnat průměru. Tím pádem jedno číslo se musí rovnat n.

3 roky  4 Likes
Ondra
Omlouvám se je to 7 hned objasnil proč.
Průměr je x.
n=1 Jedno číslo se musí rovnat průměru. Tedy x.
n=2 Další je průměr +7. Tedy x+7.
n=3 Poté to samé, ale do mínusu. x-7
n=4 Můžeme dosadit např. x+5.
n=7 Teď musíme dosadit aspoň 3 čísla, aby bylo nejvíc podprůměrných, ale jejich součin musí být -5. např. x+1, x+2, x+3
Potom nám vyjde průměr x.

3 roky  2 Likes
Aničník
Správná odpověď je 7, vysvětlím proč. Ve výpočtu musí být číslo o 7 menší než vámi vybraný průměr, potom tam musí být číslo o 7 větší než průměr a nakonec číslo rovno průměru. Pokud by bylo čísel pět jak tvrdí tato stránka, čísel s podprůměrnou hodnotou tam není většina. Čísel co jsou menší než průměr musí být alespoň o 2 více než těch větších než průměr. Musí jich tam tedy být 7

3 roky  1 Like




Tipy na související online kalkulačky
Hledáte pomoc s výpočtem aritmetického průměru?
Hledáte statistickou kalkulačku?
Potřebujete pomoci sčítat, zkrátít či vynásobit zlomky? Zkuste naši zlomkovou kalkulačku.

K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:

statistikaaritmetikačíslatémaÚroveň náročnosti úkolu

Související a podobné příklady: