Vzdálenost od křižovatky
Dvě přímé cesty se křižují a svírají úhel alfa = 53 stupňů 30'. Na jedné z nich stojí dva sloupy, jeden na křižovatce, druhý ve vzdálenosti 500 m od ní. Jak daleko je třeba jít od křižovatky po druhé cestě, abychom viděli oba sloupy v zorném úhlu beta?
a) alfa = beta
b) beta= 15 stupňů?
Vaše odpověď:
a) alfa = beta
b) beta= 15 stupňů?
Vaše odpověď:
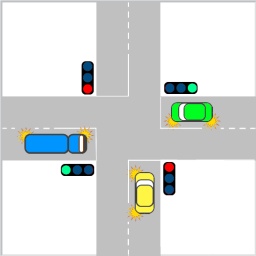
Tipy na související online kalkulačky
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
geometriealgebraplanimetrieJednotky fyzikálních veličinÚroveň náročnosti úkolu
Doporučujeme k tomuto príkladu si prohlédnout toto výukové video: video1
Související a podobné příklady:
- Dvaja
Dvě přímé čáry kříží v pravém úhlu. Dva lidé začínají současně v místě křižovatky. John jde rychlostí 4 km/h po jedné cestě a Peter jede rychlostí 8 km/h po druhé cestě. Jak dlouho bude trvat, než budou vzdálený 20√5 km od sebe? - Rovnoramenný 15
Rovnoramenný trojúhelník má velikost úhlů u základny alfa =beta=34 stupnů 34 minut. Vypočtěte ve stupních a minutách velikost úhlu u zbývajícího vrcholu trojúhelníku. - Vnější úhly trojúhelníku
ABC trojúhelník, alfa = 54stupňů 32minut, beta = 79 stupňů. Jaké jsou velikosti vnějších úhlů? - Tři sloupy
Vedle přímé cestě jsou tři sloupy vysoké 6 m ve stejné vzdálenosti 10 m. Pod jakým zorným úhlem vidí Vlado každý sloup, pokud je od prvního ve vzdálenosti 30 m a jeho oči jsou ve výšce 1,8 m? - Farmar
Farmar vidí zadní plot pozemku, který je dlouhý 50 m v zorném úhlu 30 stupňů. Od jednoho konce plotu je vzdálený 92 m. Jak daleko je od druhého konce plotu? - Z letadla
Z letadla které letí ve výšce 500 m, pozorovali ve směru letu místa A a B (nacházející se ve stejné nadmořské výšce) pod hloubkovými úhly alfa = 48° a beta = 35°. Jak daleko jsou od sebe místa A a B? - Z rozhledny
Z rozhledny vysoké 70 metrů vidíme člověka v hloubkovém úhlu 15 stupňů. Vypočítej, jak daleko od paty rozhledny člověk stojí. Nakresli a vypočítej.
