Součet 23

Součet délek všech hran kvádru jsou 4m. Přitom šířka je dvakrát kratší než délka a výška je sedmkrát delší než šířka . Urči rozměry kvádru. Děkuji lucka

Správná odpověď:

a =  0,4
b =  0,8
c =  2,8

Postup správného řešení:


a+b+c = 4
a = b/2
c = 7a

a+b+c = 4
a = b/2
c = 7·a

a+b+c = 4
2a-b = 0
7a-c = 0

Pivot: Řádek 1 ↔ Řádek 3
7a-c = 0
2a-b = 0
a+b+c = 4

Řádek 2 - 2/7 · Řádek 1 → Řádek 2
7a-c = 0
-b+0,286c = 0
a+b+c = 4

Řádek 3 - 1/7 · Řádek 1 → Řádek 3
7a-c = 0
-b+0,286c = 0
b+1,143c = 4

Řádek 3 + Řádek 2 → Řádek 3
7a-c = 0
-b+0,286c = 0
1,429c = 4


c = 4/1,42857143 = 2,8
b = 0-0,28571428571429c/-1 = 0-0,28571429 · 2,8/-1 = 0,8
a = 0+c/7 = 0+2,8/7 = 0,4

a = 2/5 = 0,4
b = 4/5 = 0,8
c = 14/5 = 2,8

Vypočtené naším kalkulátorem soustavy lineárních rovnic.

Zkusit jiný příklad


Našel jsi chybu či nepřesnost? Klidně nám ji napiš.







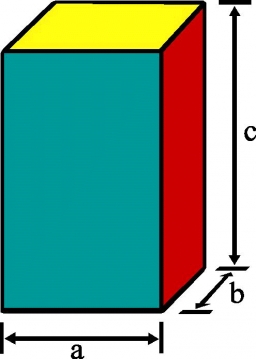
Tipy na související online kalkulačky
Máte lineární rovnici nebo soustavu rovnic a hledáte její řešení? Nebo máte kvadratickou rovnici?
Chcete proměnit jednotku délky?

K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:

Jednotky fyzikálních veličin:

Úroveň náročnosti úkolu:

Související a podobné příklady: