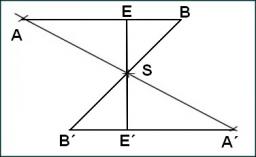
Množina bodů Z7–I–5.
Je dán trojúhelník ABC se stranami /AB/=3 cm, /BC/= 10 cm a úhlem ABC = 120°. Narýsujte všechny body X tak, aby platilo, že trojúhelník BCX je rovnoramenný a současně trojúhelník ABX je rovnoramenný se základnou AB.
Správná odpověď:
Zobrazuji 2 komentáře:
Mo - Radce
Myslim ze bod X je jenom jeden - spravis osi stran AB a BC a ich prusecnik je hledany bod X.
Mo - Radce2
No nevím; podle dohody je úhel u prostředního vrcholu, pokud je jeho název dán pomocí vrcholu trojúhelníku, tudíž úhel ABC má vrchol v bobu B, nikoliv v bodu A. V tom případě není správně délka strany BC.
Samozřejmě je pravda, že průsečíkem os stran BC a AB získám bod X, pro který platí uvedené podmínky. Tentýž bod by ale existoval i v opačné polorovině. Tahle situace platí za předpokladu, že BC je základna rovnoramenného trojúhelníku.
Pokud by BC nebyla základna, ale rameno rovnoramenného trojúhelníku, tak si myslím, že kdybych narýsoval kružnici o poloměru 10 cm se středem v bodu C, dostanu dva průsečíky s osou strany AB. Oba body X, které by vznikly, by měly vyhovovat a tytéž body by měly být i v opačné polorovině.
Když udělám tutéž kružnici se středem v bodu B, tak zase vzniknou dva průsečíky s osou strany AB, které ale budou sobě navzájem obrazem v osové souměrnosti. Takže přemýšlím o tom, že těch bodů bude celkem 8. Ještě jsem to ale nerýsoval, protože mi odešlo kružítko...
Samozřejmě je pravda, že průsečíkem os stran BC a AB získám bod X, pro který platí uvedené podmínky. Tentýž bod by ale existoval i v opačné polorovině. Tahle situace platí za předpokladu, že BC je základna rovnoramenného trojúhelníku.
Pokud by BC nebyla základna, ale rameno rovnoramenného trojúhelníku, tak si myslím, že kdybych narýsoval kružnici o poloměru 10 cm se středem v bodu C, dostanu dva průsečíky s osou strany AB. Oba body X, které by vznikly, by měly vyhovovat a tytéž body by měly být i v opačné polorovině.
Když udělám tutéž kružnici se středem v bodu B, tak zase vzniknou dva průsečíky s osou strany AB, které ale budou sobě navzájem obrazem v osové souměrnosti. Takže přemýšlím o tom, že těch bodů bude celkem 8. Ještě jsem to ale nerýsoval, protože mi odešlo kružítko...
Tipy na související online kalkulačky
Vypočet rovnoramenného trojúhelníku.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
Jednotky fyzikálních veličin:
Téma:
Úroveň náročnosti úkolu:
Doporučujeme k tomuto príkladu si prohlédnout toto výukové video: video1
Související a podobné příklady:
- Rovnoramenný trojúhelník
 Narýsujte rovnoramenný trojúhelník ABC, pokud AB = 7cm, velikost úhlu ABC je 47°, ramena | AC | = | BC |. Změřte velikost strany BC v mm.
Narýsujte rovnoramenný trojúhelník ABC, pokud AB = 7cm, velikost úhlu ABC je 47°, ramena | AC | = | BC |. Změřte velikost strany BC v mm. - Z7-1-6 MO 2018
 Je dán rovnoramenný pravoúhlý trojúhelník ABS se základnou AB. Na kružnici, která má střed v bodě S a prochází body A a B, leží bod C tak, že trojúhelník ABC je rovnoramenný. Určete, kolik bodů C vyhovuje uvedeným podmínkám, a všechny takové body sestrojt
Je dán rovnoramenný pravoúhlý trojúhelník ABS se základnou AB. Na kružnici, která má střed v bodě S a prochází body A a B, leží bod C tak, že trojúhelník ABC je rovnoramenný. Určete, kolik bodů C vyhovuje uvedeným podmínkám, a všechny takové body sestrojt - Rovnoramenný 83208
 Zastroj rovnoramenný trojúhelník ABY se základnou AB délky 5 cm a úhlem při hlavním vrcholu velikosti 50°. Zapíše postup konstrukce.
Zastroj rovnoramenný trojúhelník ABY se základnou AB délky 5 cm a úhlem při hlavním vrcholu velikosti 50°. Zapíše postup konstrukce. - Trojúhelník
 V trojúhelníku ABC se stranou BC délky 2 cm je bod K středem strany AB. Body L a M rozdělují stranu AC na tři shodné úsečky. Trojúhelník KLM je rovnoramenný s pravým úhlem u vrcholu K. Určete délky stran AB, AC trojúhelníku ABC.
V trojúhelníku ABC se stranou BC délky 2 cm je bod K středem strany AB. Body L a M rozdělují stranu AC na tři shodné úsečky. Trojúhelník KLM je rovnoramenný s pravým úhlem u vrcholu K. Určete délky stran AB, AC trojúhelníku ABC.
- Hlavní vrchol
 ABC je rovnoramenný trojúhelník se základnou BC a hlavním vrcholem A. Úhel při vrcholu A má velikost 18°. Jakou velikost bude mít úhel při vrcholu B?
ABC je rovnoramenný trojúhelník se základnou BC a hlavním vrcholem A. Úhel při vrcholu A má velikost 18°. Jakou velikost bude mít úhel při vrcholu B? - Trojúhelníku 6672
 V trojúhelníku ABC je [AB]=20cm, [BC]=10cm, A=30°. Sestroj trojúhelník A'B'C' podobný trojúhelníku ABC, pokud koeficient podobnosti je 0,5
V trojúhelníku ABC je [AB]=20cm, [BC]=10cm, A=30°. Sestroj trojúhelník A'B'C' podobný trojúhelníku ABC, pokud koeficient podobnosti je 0,5 - Odvěsny
 V pravoúhlém trojúhelníku ABC s pravým úhlem při vrcholu C známe délku strany AB = 24 cm a úhel při vrcholu B = 71°. Vypočítejte délku odvěsen trojúhelníku.
V pravoúhlém trojúhelníku ABC s pravým úhlem při vrcholu C známe délku strany AB = 24 cm a úhel při vrcholu B = 71°. Vypočítejte délku odvěsen trojúhelníku. - RR trojuhelník
 Je dán rovnoramenný trojúhelník ABC, kde AB = AC. Obvod je 64 cm a výška na základnu je 24 cm. Najděte obsah tohoto rovnoramenného trojúhelníku
Je dán rovnoramenný trojúhelník ABC, kde AB = AC. Obvod je 64 cm a výška na základnu je 24 cm. Najděte obsah tohoto rovnoramenného trojúhelníku - Těžnice 10
 Je dána úsečka AA1 délky 6 cm. Sestrojte všechny trojúhelníky ABC, pro které je AA1 těžnicí, délka strany BC je 5 cm a velikost úhlu gama je 60°.
Je dána úsečka AA1 délky 6 cm. Sestrojte všechny trojúhelníky ABC, pro které je AA1 těžnicí, délka strany BC je 5 cm a velikost úhlu gama je 60°.
- Určete 49
 Určete bod C tak, aby trojúhelník ABC byl pravoúhlý a rovnoramenný s přeponou AB, kde A[4,-6], B[-2,10]
Určete bod C tak, aby trojúhelník ABC byl pravoúhlý a rovnoramenný s přeponou AB, kde A[4,-6], B[-2,10] - Sestroj
 Sestroj rovnoběžník (kosodélník) ABCD, |AB|= 4 cm alfa=30° |BD|= 5 cm.
Sestroj rovnoběžník (kosodélník) ABCD, |AB|= 4 cm alfa=30° |BD|= 5 cm. - Podobný
 Pokud trojúhelník ABC ~ (podobný) trojúhelníku XYZ, AC = 24, AB = 15, BC = 17 a XY = 9, jaký je obvod trojúhelníku XYZ? Zaokrouhlete všechny strany na 1 desetinné místo.
Pokud trojúhelník ABC ~ (podobný) trojúhelníku XYZ, AC = 24, AB = 15, BC = 17 a XY = 9, jaký je obvod trojúhelníku XYZ? Zaokrouhlete všechny strany na 1 desetinné místo. - Trojúhelníku 60993
 V pravoúhlém trojúhelníku ABC vypočítejte velikost vnitřních úhlů, pokud/AB/ = 13 cm; /BC/ = 12 cm a/AC/ = 5 cm.
V pravoúhlém trojúhelníku ABC vypočítejte velikost vnitřních úhlů, pokud/AB/ = 13 cm; /BC/ = 12 cm a/AC/ = 5 cm. - Těžnice RR trojúhelníku
 Rovnoramenný trojúhelník ABC má základnu | AB | = 16cm a rameno délky 10cm. Jaké jsou délky těžnic?
Rovnoramenný trojúhelník ABC má základnu | AB | = 16cm a rameno délky 10cm. Jaké jsou délky těžnic?
- Dvě konstrukce
 A. Sestrojte ∆ABC takový, že c = 55 mm, α = 45°, β = 60°. B. Narýsujte libovolný ostroúhlý trojúhelník a sestrojte jeho výšky.
A. Sestrojte ∆ABC takový, že c = 55 mm, α = 45°, β = 60°. B. Narýsujte libovolný ostroúhlý trojúhelník a sestrojte jeho výšky. - Trojúhelníku 47071
 V trojúhelníku ABC, pravoúhlý úhel je na vrcholu B. Strany /AB/=7cm, /BC/=5cm, /AC/=8,6cm. Najděte na dvě desetinná místa. A. sinus úhlu C B. Kosinus C C. Tangenta C.
V trojúhelníku ABC, pravoúhlý úhel je na vrcholu B. Strany /AB/=7cm, /BC/=5cm, /AC/=8,6cm. Najděte na dvě desetinná místa. A. sinus úhlu C B. Kosinus C C. Tangenta C. - Vypočítejte 57
 Vypočítejte výšku na základnu rovnoramenného trojúhelníka ABC se základnou AB, AB = c = 10 cm a rameny a = b =13 cm
Vypočítejte výšku na základnu rovnoramenného trojúhelníka ABC se základnou AB, AB = c = 10 cm a rameny a = b =13 cm
