Fyzikální veličiny - slovní úlohy a příklady - strana 257 z 282
Počet nalezených příkladů: 5632
- Trojúhelník
 Vypočítejte obsah pravoúhlého trojúhelníku ΔABC, pokud jedna odvěsna je dlouhá 16 a protilehlý úhel je 56°.
Vypočítejte obsah pravoúhlého trojúhelníku ΔABC, pokud jedna odvěsna je dlouhá 16 a protilehlý úhel je 56°. - V jedné třetině
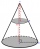 Objem pravého kruhového kužele je 5 litrů. Vypočítejte objem dvou částí, na které je kužel rozdělen rovinou rovnoběžnou se základnou, v jedné třetině vzdálenosti od vrcholu k základně.
Objem pravého kruhového kužele je 5 litrů. Vypočítejte objem dvou částí, na které je kužel rozdělen rovinou rovnoběžnou se základnou, v jedné třetině vzdálenosti od vrcholu k základně. - Trojboký hranol
 Rovina, která prochází hranou AB a středem hrany CC' pravidelného trojbokého hranolu ABCA'B'C', svírá s podstavou úhel 46 stupňů, |AB| = 12 cm. Vypočítejte objem hranolu.
Rovina, která prochází hranou AB a středem hrany CC' pravidelného trojbokého hranolu ABCA'B'C', svírá s podstavou úhel 46 stupňů, |AB| = 12 cm. Vypočítejte objem hranolu. - Výškový rozdíl
 Jaký výškový rozdíl překonáme, pokud přejdeme cestu dlouhou 1 km se stoupáním 21 promile?
Jaký výškový rozdíl překonáme, pokud přejdeme cestu dlouhou 1 km se stoupáním 21 promile? - Sáňky
 Délka sáňkařské dráhy je 60m, výška 8 m. Chlapec táhne sáňky o hmotnosti 15 kg. Jak velkou sílou táhne chlapec sáňky do kopce?
Délka sáňkařské dráhy je 60m, výška 8 m. Chlapec táhne sáňky o hmotnosti 15 kg. Jak velkou sílou táhne chlapec sáňky do kopce? - Úhel x
 Úhel x je oproti straně AB, která je dlouhá 10 a strana AC je dlouhá 15 a je přeponou v trojúhelníku ABC. Vypočtěte úhel x.
Úhel x je oproti straně AB, která je dlouhá 10 a strana AC je dlouhá 15 a je přeponou v trojúhelníku ABC. Vypočtěte úhel x. - Kosínus
 Bod [8, 6] leží na koncové straně úhlu θ. cos θ = ...
Bod [8, 6] leží na koncové straně úhlu θ. cos θ = ... - Kruh - úseč
 Kruh o průměru 30 cm je přeťat tětivou t = 16 cm. Vypočtěte obvod a obsah menší úseče.
Kruh o průměru 30 cm je přeťat tětivou t = 16 cm. Vypočtěte obvod a obsah menší úseče. - Kosinus pi/4
 Dáno w =√2(kosinus (pi/4) + i sinus (pi/4) ) a z = 2 (kosinus (pi/2) + i sinus (pi/2)), Co je w - z vyjádřeno v polární formě?
Dáno w =√2(kosinus (pi/4) + i sinus (pi/4) ) a z = 2 (kosinus (pi/2) + i sinus (pi/2)), Co je w - z vyjádřeno v polární formě? - Desaťuholník - hranol
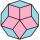 Pravidelný desaťuholník se stranou a = 2 cm je podstavou kolmého hranolu, jehož boční stěny jsou čtverce. Určete objem hranolu v cm³ s přesností na dvě desetinná místa.
Pravidelný desaťuholník se stranou a = 2 cm je podstavou kolmého hranolu, jehož boční stěny jsou čtverce. Určete objem hranolu v cm³ s přesností na dvě desetinná místa. - Pacienti
 Přípravek úspěšně léčí 90% případů. Vypočítejte pravděpodobnost, že vyléčí alespoň 18 pacientů z 20ti?
Přípravek úspěšně léčí 90% případů. Vypočítejte pravděpodobnost, že vyléčí alespoň 18 pacientů z 20ti? - Reflektor
 Kruhový reflektor vrhá světelný kužel s vrcholovým úhlem o velikosti 46° a je zavěšen ve výšce 30 m na stožáru tak, že osa světelného kužele svírá s osou stožáru úhel o velikosti 15°. Jakou největší délku osvětlí reflektor na vodorovné rovině?
Kruhový reflektor vrhá světelný kužel s vrcholovým úhlem o velikosti 46° a je zavěšen ve výšce 30 m na stožáru tak, že osa světelného kužele svírá s osou stožáru úhel o velikosti 15°. Jakou největší délku osvětlí reflektor na vodorovné rovině? - Kosodélník
 Vypočítejte obsah a obvod kosodélníku s délkou stran 19 a 11, které svírají úhel 30°.
Vypočítejte obsah a obvod kosodélníku s délkou stran 19 a 11, které svírají úhel 30°. - Rovnoramenný pravoúhlý
 Vypočítejte obsah rovnoramenného pravoúhlého trojúhelníku, jehož obvod je 670 cm.
Vypočítejte obsah rovnoramenného pravoúhlého trojúhelníku, jehož obvod je 670 cm. - Nepřístupna místa
 Určete vzdálenost dvou nepřístupných míst K, L, pokud se z bodů A, B, které jsou od sebe vzdáleny 870 m, naměřily velikosti úhlů KAL=62°10", LAB=41°23", KBL=66°34", LBA = 34°52". Děkuji.
Určete vzdálenost dvou nepřístupných míst K, L, pokud se z bodů A, B, které jsou od sebe vzdáleny 870 m, naměřily velikosti úhlů KAL=62°10", LAB=41°23", KBL=66°34", LBA = 34°52". Děkuji. - Sluneční paprsky
 Dopadají-li sluneční paprsky pod úhlem 60°, vrhá slavná egyptská Cheopsova pyramida, která je dnes vysoká 137,3m, stín dlouhý 79,3m. Vypočítejte dnešní výšku sousední Chefrenovi pyramidy, jejíž stín měří v témže okamžiku 78,8 m, a dnešní výšku nedaleké Mi
Dopadají-li sluneční paprsky pod úhlem 60°, vrhá slavná egyptská Cheopsova pyramida, která je dnes vysoká 137,3m, stín dlouhý 79,3m. Vypočítejte dnešní výšku sousední Chefrenovi pyramidy, jejíž stín měří v témže okamžiku 78,8 m, a dnešní výšku nedaleké Mi - Pohár s džusem
 Pohár tvaru válce výšky 19 cm a průměru podstavy 7 cm je naplněn džusem tak že hladina je 3 cm pod okrajem sklenice. Určitě maximální úhel o který lze pohár naklonit tak aby se džus nevylil.
Pohár tvaru válce výšky 19 cm a průměru podstavy 7 cm je naplněn džusem tak že hladina je 3 cm pod okrajem sklenice. Určitě maximální úhel o který lze pohár naklonit tak aby se džus nevylil. - Pravoúhlý 19
 Pravoúhlý trojúhelník. Je dáno: strana c=15,8 a úhel alfa=73°10' Výpočtete stranu a, b, úhel beta a obsah.
Pravoúhlý trojúhelník. Je dáno: strana c=15,8 a úhel alfa=73°10' Výpočtete stranu a, b, úhel beta a obsah. - Porucha TV
 Televizor má za 10000 hodín v průměru 20 poruch. Určete pravděpodobnost poruchy televizoru za 700 hodin provozu.
Televizor má za 10000 hodín v průměru 20 poruch. Určete pravděpodobnost poruchy televizoru za 700 hodin provozu. - Tramvajová úloha
 Jaký je maximální úhel pod kterým může jet tramvaj z kopce dolů, aby stále byla schopna zastavit. Součinitel smykového tření je f =0,15.
Jaký je maximální úhel pod kterým může jet tramvaj z kopce dolů, aby stále byla schopna zastavit. Součinitel smykového tření je f =0,15.
Máš příklad z matematiky, který jsi tady nenašel vyřešený? Pošli nám příklad a my Ti ho zkusíme vypočítat.
