Sluneční paprsky
Dopadají-li sluneční paprsky pod úhlem 60°, vrhá slavná egyptská Cheopsova pyramida, která je dnes vysoká 137,3m, stín dlouhý 79,3m. Vypočítejte dnešní výšku sousední Chefrenovi pyramidy, jejíž stín měří v témže okamžiku 78,8 m, a dnešní výšku nedaleké Mikerinovi pyramidy, která ve stejný čas vrhá stín dlouhý 35,8m.
Správná odpověď:

Zobrazuji 3 komentáře:
Žák
V druhem kroku jsem len prepočítal či slnce sviti pod uhlom 60 stupňu... Nepovinny krok
8 let 2 Likes
Dr Math
Ano, upravili sme globalne ze arctan je medzinarodna/anglicka skratka pre arkustangens.... v nasich koncinach je spravnejsi pouzivet arctg...
Tipy na související online kalkulačky
Vyzkoušejte naši kalkulačka na přepočet poměru.
Chcete proměnit jednotku délky?
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte si převody jednotek úhlů úhlové stupně, minuty, sekundy, radiány.
Chcete proměnit jednotku délky?
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte si převody jednotek úhlů úhlové stupně, minuty, sekundy, radiány.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
geometriestereometrieplanimetriezákladní operace a pojmygoniometrie a trigonometrieJednotky fyzikálních veličinÚroveň náročnosti úkolu
Související a podobné příklady:
- Budova
 Jak vysoká je budova, která na vodorovnou dlažbu vrhá stín dlouhý 62,8 m pod uhlom 36°18'?
Jak vysoká je budova, která na vodorovnou dlažbu vrhá stín dlouhý 62,8 m pod uhlom 36°18'? - Vypočtěte 19
 Vypočtěte výšku stromu, který vrhá stín délky 22 m, víte-li, že ve stejném okamžiku pilíř vysoký 2 m vrhá stín dlouhý 3metry.
Vypočtěte výšku stromu, který vrhá stín délky 22 m, víte-li, že ve stejném okamžiku pilíř vysoký 2 m vrhá stín dlouhý 3metry. - Stožár
 Stožár elektrického vedení vrhá 17 m dlouhý stín na stráň která stoupá od paty stožáru ve směru stínu pod úhlem o velikosti 5,3°.Určete výšku stožáru jestliže výška Slunce nad obzorem je 40°48'.
Stožár elektrického vedení vrhá 17 m dlouhý stín na stráň která stoupá od paty stožáru ve směru stínu pod úhlem o velikosti 5,3°.Určete výšku stožáru jestliže výška Slunce nad obzorem je 40°48'. - Pravoúhlý 33
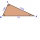 Pravoúhlý trojúhelník KLM s pravým úhlem při vrcholu L, uhlem beta při vrcholu K a uhlem alfa u vrcholu M. Úhel u vrcholu M = 65°, strana l = 17,5 cm. Pomoci Pythagorovy věty a goniometrických funkci vypočítáte délky všech stran a úhel při vrcholu K.
Pravoúhlý trojúhelník KLM s pravým úhlem při vrcholu L, uhlem beta při vrcholu K a uhlem alfa u vrcholu M. Úhel u vrcholu M = 65°, strana l = 17,5 cm. Pomoci Pythagorovy věty a goniometrických funkci vypočítáte délky všech stran a úhel při vrcholu K. - Rozhledna 3
 Jak vysoká je rozhledna, jestliže vrhá stín dlouhý 9,6m přesně ve stejném okamžiku, kdy puůlmetrová tyč vrhá stín dlouhý 30 cm.
Jak vysoká je rozhledna, jestliže vrhá stín dlouhý 9,6m přesně ve stejném okamžiku, kdy puůlmetrová tyč vrhá stín dlouhý 30 cm. - Velikost přepony trojúhelníku
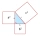 Je dán pravoúhlý trojúhelník KLM s pravým úhlem u M. Jaká je velikost přepony m, pokud velikost těžnice na přeponu m je 4.
Je dán pravoúhlý trojúhelník KLM s pravým úhlem u M. Jaká je velikost přepony m, pokud velikost těžnice na přeponu m je 4. - Svislá
 Svislá metrová tyč vrhá stín 150 cm dlouhý. Vypočtěte výšku sloupu, jehož stín je ve stejném okamžiku 36 m dlouhý.
Svislá metrová tyč vrhá stín 150 cm dlouhý. Vypočtěte výšku sloupu, jehož stín je ve stejném okamžiku 36 m dlouhý.
