Fyzikální veličiny - slovní úlohy a příklady - strana 256 z 282
Počet nalezených příkladů: 5632
- Tunel - čtyřúhelník
 Jak dlouhý bude tunel AB, vzdálenosti AD=35 m, DC=120 m, CB=85 m a úhly ADC=105 stupňů a BCD=71 stupňů. ABCD je čtyřúhelník.
Jak dlouhý bude tunel AB, vzdálenosti AD=35 m, DC=120 m, CB=85 m a úhly ADC=105 stupňů a BCD=71 stupňů. ABCD je čtyřúhelník. - Obsah
 Vypočítejte obsah čtyřúhelníku, jehož dvě a dvě strany jsou stejně dlouhé a rovnoběžné o délkách stran 7, 9, 7 a 9. Vnitřní úhly čtyřúhelníku jsou 45°, 135°,45°, 135°.
Vypočítejte obsah čtyřúhelníku, jehož dvě a dvě strany jsou stejně dlouhé a rovnoběžné o délkách stran 7, 9, 7 a 9. Vnitřní úhly čtyřúhelníku jsou 45°, 135°,45°, 135°. - Velikost úhlů
 V pravoúhlém trojúhelníku ABC vypočítejte velikost vnitřních úhlů, pokud/AB/ = 13 cm; /BC/ = 12 cm a/AC/ = 5 cm.
V pravoúhlém trojúhelníku ABC vypočítejte velikost vnitřních úhlů, pokud/AB/ = 13 cm; /BC/ = 12 cm a/AC/ = 5 cm. - Nepodráždil obojek
 Alžbětinský obojek se používá k tomu, aby si zvíře nepodráždilo ránu. Úhel mezi otvorem (průměr 6 palců) a koncem (o průměru 16 palců) svírá se stranou límce úhel 53 stupňů. Najděte uvedenou plochu límce.
Alžbětinský obojek se používá k tomu, aby si zvíře nepodráždilo ránu. Úhel mezi otvorem (průměr 6 palců) a koncem (o průměru 16 palců) svírá se stranou límce úhel 53 stupňů. Najděte uvedenou plochu límce. - Vypočítejte
 Vypočítejte délku tětivy v kružnici o poloměru 25 cm, které přísluší obvodový úhel 26°.
Vypočítejte délku tětivy v kružnici o poloměru 25 cm, které přísluší obvodový úhel 26°. - Moivrovka
 Existují dvě různá komplexní čísla z taková, že z na třetí se rovná 1 a současně z není rovno 1. Vypočtěte součet těchto dvou čísel.
Existují dvě různá komplexní čísla z taková, že z na třetí se rovná 1 a současně z není rovno 1. Vypočtěte součet těchto dvou čísel. - Úhlopříčky
 Vypočítejte délky úhlopříček v kosočtverci, jestliže jeho strana má délku 13 a jeden jeho vnitřní úhel je 80°.
Vypočítejte délky úhlopříček v kosočtverci, jestliže jeho strana má délku 13 a jeden jeho vnitřní úhel je 80°. - Vzdálenosti - majáky
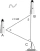 Dva majáky A, B spatřily loď, jak je znázorněno na obrázku. Jaká je vzdálenost mezi lodí a majákem A s přesností na jednu desetinu námořní míle? Obrázek - vzdálenost mezi majáky A a B je 40 námořních mil. Z bodu A je vidět úhel pohledu 57° a z bodu B pod
Dva majáky A, B spatřily loď, jak je znázorněno na obrázku. Jaká je vzdálenost mezi lodí a majákem A s přesností na jednu desetinu námořní míle? Obrázek - vzdálenost mezi majáky A a B je 40 námořních mil. Z bodu A je vidět úhel pohledu 57° a z bodu B pod - Komolý jehlan
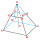 Vypočítejte objem pravidelného 4-bokeho komolého jehlanu, jestliže a1 = 14 cm, a2 = 8 cm a úhel, který svírá boční stěna s podstavou je 42 stupňů.
Vypočítejte objem pravidelného 4-bokeho komolého jehlanu, jestliže a1 = 14 cm, a2 = 8 cm a úhel, který svírá boční stěna s podstavou je 42 stupňů. - Velikost úhlu α v trojúhelníku
 V pravoúhlém trojúhelníku ABC přepona c = 8 cm a odvěsna b = 4 cm. Jaká je velikost úhlu α?
V pravoúhlém trojúhelníku ABC přepona c = 8 cm a odvěsna b = 4 cm. Jaká je velikost úhlu α? - 12 úhelník
 Vypočtěte obsah pravidelného 12 úhelníka, je-li jeho strana a=12 cm.
Vypočtěte obsah pravidelného 12 úhelníka, je-li jeho strana a=12 cm. - Těžnice RR trojúhelníku
 Rovnoramenný trojúhelník ABC má základnu | AB | = 16cm a rameno délky 10cm. Jaké jsou délky těžnic?
Rovnoramenný trojúhelník ABC má základnu | AB | = 16cm a rameno délky 10cm. Jaké jsou délky těžnic? - Sklon žebříku
 Jaký je sklon žebříku 6,2m a opřen je ve výšce 5,12m.
Jaký je sklon žebříku 6,2m a opřen je ve výšce 5,12m. - Zkosení
 Mám zápis zkosení v poměru 1:6. Jaký je úhel a jaké ho vypočítám?
Mám zápis zkosení v poměru 1:6. Jaký je úhel a jaké ho vypočítám? - Tělesová
 Tělesová úhlopříčka pravidelného čtyřbokého hranolu svírá s podstavou úhel velikosti 60°. Hrana podstavy má délku 10cm. Vypočítejte objem tělesa.
Tělesová úhlopříčka pravidelného čtyřbokého hranolu svírá s podstavou úhel velikosti 60°. Hrana podstavy má délku 10cm. Vypočítejte objem tělesa. - Trojúhelník ABC 2
 Trojúhelník ABC má délky stran a = 14 cm, b = 20 cm, c = 7,5 cm. Zjisti velikosti úhlů a obsah tohoto trojúhelníku.
Trojúhelník ABC má délky stran a = 14 cm, b = 20 cm, c = 7,5 cm. Zjisti velikosti úhlů a obsah tohoto trojúhelníku. - n-úhelník
 Jaká je délka strany pravidelného 8-úhelníku vepsaného do kružnice o poloměru 8 cm?
Jaká je délka strany pravidelného 8-úhelníku vepsaného do kružnice o poloměru 8 cm? - Trojúhelník a jeho výšky
 Vypočítejte délky stran trojúhelníku ABC, jestliže va=10 cm, vb=11 cm a strana b je o 5 cm kratší než strana a.
Vypočítejte délky stran trojúhelníku ABC, jestliže va=10 cm, vb=11 cm a strana b je o 5 cm kratší než strana a. - Cena střechy
 Přístřešek na auto je třeba přikrýt valbovou střechou s obdélníkovým průřezem 8 m x 5 m. Všechny střešní plochy mají stejný sklon 30°. Určete cenu a hmotnost střechy, pokud 1 m² stojí 270 € a váží 43 kg.
Přístřešek na auto je třeba přikrýt valbovou střechou s obdélníkovým průřezem 8 m x 5 m. Všechny střešní plochy mají stejný sklon 30°. Určete cenu a hmotnost střechy, pokud 1 m² stojí 270 € a váží 43 kg. - ABC - 2SU
 Řešte trojúhelník ABC je-li dáno: A = 50°, b = 13, c = 6
Řešte trojúhelník ABC je-li dáno: A = 50°, b = 13, c = 6
Máš úkol, který jsi tady nenašel vyřešen? Pošli nám úkol a my Ti ji zkusíme vypočítat. Řešení příkladů z matematiky.
