Goniometrie a trigonometrie - slovní úlohy a příklady - strana 25 z 32
Počet nalezených příkladů: 627
- V rovině 2
 V rovině je umístěn trojúhelník ABC s pravým úhlem u vrcholu C, pro který platí: A(1, 2), B(5, 2), C(x, x+1), kde x > -1. a) určete hodnotu x b) určete souřadnice bodu M, který je středem úsečky AB c) dokažte že vektory AB a CM jsou kolmé d) určete vel
V rovině je umístěn trojúhelník ABC s pravým úhlem u vrcholu C, pro který platí: A(1, 2), B(5, 2), C(x, x+1), kde x > -1. a) určete hodnotu x b) určete souřadnice bodu M, který je středem úsečky AB c) dokažte že vektory AB a CM jsou kolmé d) určete vel - Vypočtěte 12
 Vypočtěte povrch a objem pravidelného devítibokého jehlanu, měří-li poloměr kružnice vepsané podstavě ρ= 12 cm a výška jehlanu je 24 cm
Vypočtěte povrch a objem pravidelného devítibokého jehlanu, měří-li poloměr kružnice vepsané podstavě ρ= 12 cm a výška jehlanu je 24 cm - Stožár
 Stožár má 13 metrů dlouhý stín na svahu stoupajícím od sloupu sloupku ve směru úhlu stínu při úhlu 15°. Určete výšku stožáru, pokud je slunce nad obzorem (horizontem) v úhlu 33°. Použijte sinusovou větu.
Stožár má 13 metrů dlouhý stín na svahu stoupajícím od sloupu sloupku ve směru úhlu stínu při úhlu 15°. Určete výšku stožáru, pokud je slunce nad obzorem (horizontem) v úhlu 33°. Použijte sinusovou větu. - Nepřístupne místa
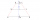 Určete vzdálenost dvou nepřístupných míst P, Q, pokud vzdálenost dvou pozorovacích míst A, B je 2000m a znáte-li velikost úhlů QAB = 52°40'; PBA = 42°01'; PAB = 86°40' a QBA = 81°15'. Uvažovaná místa A, B, P, Q leží v jedné rovině.
Určete vzdálenost dvou nepřístupných míst P, Q, pokud vzdálenost dvou pozorovacích míst A, B je 2000m a znáte-li velikost úhlů QAB = 52°40'; PBA = 42°01'; PAB = 86°40' a QBA = 81°15'. Uvažovaná místa A, B, P, Q leží v jedné rovině. - Úhel
 Objem rotačního kužele je 9,42 cm3, přičemž výška je rovna 10 cm. Jaký úhel svírá strana kužele s rovinnou podstavy?
Objem rotačního kužele je 9,42 cm3, přičemž výška je rovna 10 cm. Jaký úhel svírá strana kužele s rovinnou podstavy? - Valec naležato
 Válec o průměru 3m a výšce/délce 15 m je položen naležato. Je do něj napuštěna voda, která sahá do výšky 60 cm pod osu válce. Kolik hektolitrů vody je ve válci?
Válec o průměru 3m a výšce/délce 15 m je položen naležato. Je do něj napuštěna voda, která sahá do výšky 60 cm pod osu válce. Kolik hektolitrů vody je ve válci? - Urči hodnotu
 Urči hodnotu funkce tg x, když cotg x = -0,8; x platí že je v druhém kvadrantu)
Urči hodnotu funkce tg x, když cotg x = -0,8; x platí že je v druhém kvadrantu) - Vypočtěte
 Vypočtěte největší úhel trojúhelníku, jehož strany mají velikost: 2a, 3/2a, 3a
Vypočtěte největší úhel trojúhelníku, jehož strany mají velikost: 2a, 3/2a, 3a - Rovnoramenný - osy uhlov
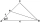 V rovnoramenném trojúhelníku ABC se základnou AB platí ∠BAC = 20°, AB = 4. Osa vnitřního úhlu u vrcholu B protíná stranu AC v bodě P. Vypočítejte délku úsečky AP. Výsledek uveďte s přesností na dvě desetinná místa.
V rovnoramenném trojúhelníku ABC se základnou AB platí ∠BAC = 20°, AB = 4. Osa vnitřního úhlu u vrcholu B protíná stranu AC v bodě P. Vypočítejte délku úsečky AP. Výsledek uveďte s přesností na dvě desetinná místa. - Úhel stoupání cesty
 Rovná cesta má stoupání 19%. Jak velký je úhel stoupání?
Rovná cesta má stoupání 19%. Jak velký je úhel stoupání? - Tvrdé dřevo
 Tvrdé dřevo pro sloup je ve tvaru komolého jehlanu, pravidelné heptagonálnej (hepta = 7) pyramidy. Dolní hrana základny je 18 cm a horní základna 14 cm. Výška je 30 cm. Zjistěte jeho hmotnost v kg, pokud je hustota dřeva 10 gramů / cm³.
Tvrdé dřevo pro sloup je ve tvaru komolého jehlanu, pravidelné heptagonálnej (hepta = 7) pyramidy. Dolní hrana základny je 18 cm a horní základna 14 cm. Výška je 30 cm. Zjistěte jeho hmotnost v kg, pokud je hustota dřeva 10 gramů / cm³. - Koule ve kuželi
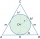 Do kužele je vepsána koule (průnik jejich hranic se skládá z kružnice a jednoho bodu). Poměr povrchu koule a obsahu podstavy je 4:3. Rovina, která prochází osou kužele, řeže kužel v rovnoramenném trojúhelníku. Určete velikost úhlu oproti základně tohoto t
Do kužele je vepsána koule (průnik jejich hranic se skládá z kružnice a jednoho bodu). Poměr povrchu koule a obsahu podstavy je 4:3. Rovina, která prochází osou kužele, řeže kužel v rovnoramenném trojúhelníku. Určete velikost úhlu oproti základně tohoto t - Do rovnostranného
 Do rovnostranného trojúhelníku se stranou 10 cm je vepsán čtverec. Vypočítejte délku strany čtverce.
Do rovnostranného trojúhelníku se stranou 10 cm je vepsán čtverec. Vypočítejte délku strany čtverce. - Odmocnina - tětiva
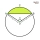 Tětiva o délce t = r krát druhá odmocnina dva rozděluje, kruh o poloměru r na dva kruhové odseky. V jakém poměru jsou obsahy těchto odseků?
Tětiva o délce t = r krát druhá odmocnina dva rozděluje, kruh o poloměru r na dva kruhové odseky. V jakém poměru jsou obsahy těchto odseků? - Vektory - skalárně
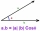 Dány jsou vektory a = (3, -2), b = (-1, 5). Určete vektor c, pro který platí a. c = 17; b.c = 3
Dány jsou vektory a = (3, -2), b = (-1, 5). Určete vektor c, pro který platí a. c = 17; b.c = 3 - Dvě síly
 Dvě síly F1 = 580N a F2 = 630N svírají úhel 59 stupňů. Vypočítejte jejich výslednici F.
Dvě síly F1 = 580N a F2 = 630N svírají úhel 59 stupňů. Vypočítejte jejich výslednici F. - Koeficient a v rovnici přímky
 V rovnici přímky p: ax-2y+1=0 určete koeficient a tak, aby přímka p: a) svírala s kladným směrem osy x úhel 120°, b) procházela bodem A[3,-2], c) byla rovnoběžná s osou x, d) měla směrnici k = 4.
V rovnici přímky p: ax-2y+1=0 určete koeficient a tak, aby přímka p: a) svírala s kladným směrem osy x úhel 120°, b) procházela bodem A[3,-2], c) byla rovnoběžná s osou x, d) měla směrnici k = 4. - Kostka - úhly
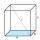 Vypočítejte úhel alfa (α) mezi stěnovou úhlopříčkou a podstavou krychle. Vypočítejte úhel beta (β) mezi tělesových úhlopříčkou a podstavou krychle.
Vypočítejte úhel alfa (α) mezi stěnovou úhlopříčkou a podstavou krychle. Vypočítejte úhel beta (β) mezi tělesových úhlopříčkou a podstavou krychle. - Horní a Dolní Ves
 Vzdálenost vzdušnou čarou mezi Dolní a Horní Vsí je 3 km a rovnoměrné stoupání je 5%. Jaký je výškový rozdíl mezi Horní a Dolní Vsí zaokrouhlený na celé metry?
Vzdálenost vzdušnou čarou mezi Dolní a Horní Vsí je 3 km a rovnoměrné stoupání je 5%. Jaký je výškový rozdíl mezi Horní a Dolní Vsí zaokrouhlený na celé metry? - Souřadnicova soustava
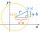 V kartézské souřadnicové soustavě je dána jednotková kružnice, na které leží body A a B. Bod O je počátek a má souřadnice (0,0) a bod B souřadnice (1,0). Velikost úhlu BOA je 151°. Určete x-ovou souřadnici bodu A.
V kartézské souřadnicové soustavě je dána jednotková kružnice, na které leží body A a B. Bod O je počátek a má souřadnice (0,0) a bod B souřadnice (1,0). Velikost úhlu BOA je 151°. Určete x-ovou souřadnici bodu A.
Máš příklad z matematiky, který jsi tady nenašel vyřešený? Pošli nám příklad a my Ti ho zkusíme vypočítat.
