Vypočtěte

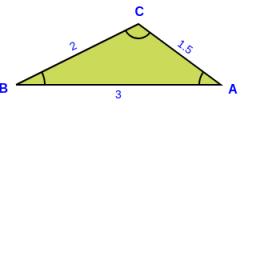
Vypočtěte největší úhel trojúhelníku, jehož strany mají velikost:
2a, 3/2a, 3a

Správná odpověď:

γ =  117,2796 °

Postup správného řešení:

x=1 a=2⋅ x=2⋅ 1=2 b=3/2⋅ x=3/2⋅ 1=23​=1,5 c=3⋅ x=3⋅ 1=3  c>a>b => γ>α>β  c2 = a2+b2 − 2⋅ a⋅ b⋅ cos γ  C=arccos(2⋅ a⋅ ba2+b2−c2​)=arccos(2⋅ 2⋅ 1,522+1,52−32​)≐2,0469 rad  γ=C→  °=C⋅ π180​   °=2,0469⋅ π180​   °=117,28  °=117,2796∘=117°16′47"

Vyzkoušejte výpočet přes naší kalkulačku trojúhelníků.


Zkusit jiný příklad


Našel jsi chybu či nepřesnost? Klidně nám ji napiš.







Tipy na související online kalkulačky
Naše kalkulačka pro výpočet procent Vám pomůže rychle vypočítat různé typické úlohy s procenty.
Máte soustavu rovnic a hledáte kalkulačku soustavy lineárních rovnic?
Pythagorova věta je základ výpočtů kalkulačky pravouhlého trojuholníka.
Kosinovú větu přímo používá kalkulačka SUS trojúhelníku.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte si převody jednotek úhlů úhlové stupně, minuty, sekundy, radiány.

K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:

algebraplanimetriezákladní operace a pojmygoniometrie a trigonometrieJednotky fyzikálních veličinÚroveň náročnosti úkolu

 
Doporučujeme k tomuto príkladu si prohlédnout toto výukové video: video1

Související a podobné příklady: