Příklady na obsah rovinných útvarů - strana 75 z 131
Počet nalezených příkladů: 2608
- Rana
 Peter si přelepil ránu dvěma náplastmi ve tvaru obdélníku (jednu přes druhou tak, že vytvořili písmeno X). Plocha zalepená současně oběma náplně měla obsah 40cm² a obvod 30cm. Jedna z náplastí byla široká 8cm. Jakou šířku měla druhá náplast?
Peter si přelepil ránu dvěma náplastmi ve tvaru obdélníku (jednu přes druhou tak, že vytvořili písmeno X). Plocha zalepená současně oběma náplně měla obsah 40cm² a obvod 30cm. Jedna z náplastí byla široká 8cm. Jakou šířku měla druhá náplast? - MO - trojúhelníky
 Na stranách AB a AC trojúhelníku ABC lěží po řadě body E a F, na úsečce EF leží bod D. Přmky EF a BC jsou rovnoběžné a součastně platí FD : DE = AE : EB = 2:1. Trojúhelník ABC má obsah 27 hektarů a úsečkami EF, AD a DB je rozdělen na čtyři části . Určete
Na stranách AB a AC trojúhelníku ABC lěží po řadě body E a F, na úsečce EF leží bod D. Přmky EF a BC jsou rovnoběžné a součastně platí FD : DE = AE : EB = 2:1. Trojúhelník ABC má obsah 27 hektarů a úsečkami EF, AD a DB je rozdělen na čtyři části . Určete - Šestiúhelník nepravidelný
 Na obrázku je čtverec ABCD, čtverec EF GD a obdélník HIJD. Body J a G leží na straně CD, přičemž platí |DJ| < |DG|, a body H a E leží na straně DA, přičemž platí |DH| < |DE|. Dále víme, že |DJ| = |GC|. Šestiúhelník ABCGFE má obvod 96 cm, šestiúhelní
Na obrázku je čtverec ABCD, čtverec EF GD a obdélník HIJD. Body J a G leží na straně CD, přičemž platí |DJ| < |DG|, a body H a E leží na straně DA, přičemž platí |DH| < |DE|. Dále víme, že |DJ| = |GC|. Šestiúhelník ABCGFE má obvod 96 cm, šestiúhelní - Kachlička
 Vypočítejte obsah plochy vyzděné ve třech řadách po 7 kusech kachličkami. Jedna kachlička je 30 cm široká a 45 cm vysoká a na dvou koncích ukončena kruhovými oblouky. Výsledek uveďte v m².
Vypočítejte obsah plochy vyzděné ve třech řadách po 7 kusech kachličkami. Jedna kachlička je 30 cm široká a 45 cm vysoká a na dvou koncích ukončena kruhovými oblouky. Výsledek uveďte v m². - Lichoběžník - úhlopříčky
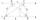 Lichoběžník má délku úhlopříčky AC přeseknutu úhlopříčkou BD v poměru 2:1. Trojúhelník vytvořen body A, průnikem úhlopříček (S) a bodem D má obsah 164 cm². (Tomuto trojúhelníku také patří strana úhlopříčky AC a je 2x větší než její druhá část.) Jaký je ob
Lichoběžník má délku úhlopříčky AC přeseknutu úhlopříčkou BD v poměru 2:1. Trojúhelník vytvořen body A, průnikem úhlopříček (S) a bodem D má obsah 164 cm². (Tomuto trojúhelníku také patří strana úhlopříčky AC a je 2x větší než její druhá část.) Jaký je ob - Čtvercova sít
 Čtvercova síť se skladá ze čtverců se stranou delky 1cm. Narysujte do ní alespoň tři různe obrazce takové, aby každý měl obsah 6cm² a obvod 12cm a aby jejich strany splývaly s přímkami síťe.
Čtvercova síť se skladá ze čtverců se stranou delky 1cm. Narysujte do ní alespoň tři různe obrazce takové, aby každý měl obsah 6cm² a obvod 12cm a aby jejich strany splývaly s přímkami síťe. - MO Z6-I-2 2017
 Erika chtěla nabídnout čokoládu svým třem kamarádkám. Když ji vytáhla z batohu, zjistila, že je polámaná jako na obrázku. (Vyznačené čtverečky jsou navzájem shodné.) Dívky se dohodly, že čokoládu dále lámat nebudou a losem určí, jak velký kousek která dos
Erika chtěla nabídnout čokoládu svým třem kamarádkám. Když ji vytáhla z batohu, zjistila, že je polámaná jako na obrázku. (Vyznačené čtverečky jsou navzájem shodné.) Dívky se dohodly, že čokoládu dále lámat nebudou a losem určí, jak velký kousek která dos - Pan Cuketa
 Pan Cuketa měl obdelníkovou zahradu. jejíž obvod byl 28 metrů. Obsah celé zahrady vyplnily právě čtyři čtvercové záhony, jejichž rozměry v metrech byly vyjádřeny celými čísly. Určete, jaké rozměry mohla mít zahrada. najděte všechny možnosti a zapište n ja
Pan Cuketa měl obdelníkovou zahradu. jejíž obvod byl 28 metrů. Obsah celé zahrady vyplnily právě čtyři čtvercové záhony, jejichž rozměry v metrech byly vyjádřeny celými čísly. Určete, jaké rozměry mohla mít zahrada. najděte všechny možnosti a zapište n ja - Z9 – I – 2 MO 2018
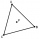 V rovnostranném trojúhelníku ABC je K středem strany AB, bod L leží v třetině strany BC blíže bodu C a bod M leží v třetině strany AC blíže bodu A. Určete, jakou část obsahu trojúhelníku ABC zabírá trojúhelník KLM.
V rovnostranném trojúhelníku ABC je K středem strany AB, bod L leží v třetině strany BC blíže bodu C a bod M leží v třetině strany AC blíže bodu A. Určete, jakou část obsahu trojúhelníku ABC zabírá trojúhelník KLM. - Jak rozdělit
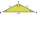 Jak rozdělit rovnoramenný trojúhelník na dvě části o stejných obsazích kolmo na osu souměrnosti (na lichoběžník a trojúhelník)?
Jak rozdělit rovnoramenný trojúhelník na dvě části o stejných obsazích kolmo na osu souměrnosti (na lichoběžník a trojúhelník)? - Z6-I-6 MO 2018
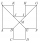 Ve dvanáctiúhelníku ABCDEF GHIJKL jsou každé dvě sousední strany kolmé a všechny strany s výjimkou stran AL a GF jsou navzájem shodné. Strany AL a GF jsou oproti ostatním stranám dvojnásobně dlouhé. Úsečky BG a EL se protínají v bodě M a rozdělují dvanáct
Ve dvanáctiúhelníku ABCDEF GHIJKL jsou každé dvě sousední strany kolmé a všechny strany s výjimkou stran AL a GF jsou navzájem shodné. Strany AL a GF jsou oproti ostatním stranám dvojnásobně dlouhé. Úsečky BG a EL se protínají v bodě M a rozdělují dvanáct - Z7–I–2 MO 2017
 Jsou dány dvě dvojice rovnoběžných přímek AB k CD a AC k BD. Bod E leží na přímce BD, bod F je středem úsečky BD, bod G je středem úsečky CD a obsah trojúhelníku ACE je 20 cm². Určete obsah trojúhelníku DFG.
Jsou dány dvě dvojice rovnoběžných přímek AB k CD a AC k BD. Bod E leží na přímce BD, bod F je středem úsečky BD, bod G je středem úsečky CD a obsah trojúhelníku ACE je 20 cm². Určete obsah trojúhelníku DFG. - Parabolická
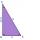
 Parabolická úseč má základnu a= 4 cm a výšku v= 6 cm. Vypočítejte objem tělesa, které vznikne rotací této úseče a) kolem své základny b) kolem své osy. Předem děkuji za řešení.
Parabolická úseč má základnu a= 4 cm a výšku v= 6 cm. Vypočítejte objem tělesa, které vznikne rotací této úseče a) kolem své základny b) kolem své osy. Předem děkuji za řešení. - V lichoběžníku
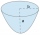
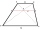 V lichoběžníku ABCD jsou dány základny: AB = 12cm CD = 4 cm A úhlopříčky se protínají pod pravým úhlem. Jaký je obsah tohoto lichoběžníku ABCD?
V lichoběžníku ABCD jsou dány základny: AB = 12cm CD = 4 cm A úhlopříčky se protínají pod pravým úhlem. Jaký je obsah tohoto lichoběžníku ABCD? - Bazén 22
 Bazén o délce l = 50 m a šířce s = 15 m má u stěny v nejmělčí části hloubku h1 = 1,2 m. Hloubka se pak plynule zvětšuje do hloubky h2 = 1,5 m uprostřed bazénu a dál se opět plynule zvětšuje do hloubky h3 = 4,5 m u stěny v nejhlubší části bazénu. Uvažujte
Bazén o délce l = 50 m a šířce s = 15 m má u stěny v nejmělčí části hloubku h1 = 1,2 m. Hloubka se pak plynule zvětšuje do hloubky h2 = 1,5 m uprostřed bazénu a dál se opět plynule zvětšuje do hloubky h3 = 4,5 m u stěny v nejhlubší části bazénu. Uvažujte - Přívalový déšť
 Na fotbalové hřiště o rozměrech 110m x 70m přišel přívalový déšť a během 15 minut napršela voda do výšky 80 mm na každý m². Hřiště je konstruováno tak, že je odvodněno a voda může odtékat 4 kanály, každý o vnitřním průřezu 7,2 dm². Jak velký objem vody od
Na fotbalové hřiště o rozměrech 110m x 70m přišel přívalový déšť a během 15 minut napršela voda do výšky 80 mm na každý m². Hřiště je konstruováno tak, že je odvodněno a voda může odtékat 4 kanály, každý o vnitřním průřezu 7,2 dm². Jak velký objem vody od - Terezka
 Krychle má obsah podstavy 289 mm². Vypočítej její délku hrany, objem a povrh plášte.
Krychle má obsah podstavy 289 mm². Vypočítej její délku hrany, objem a povrh plášte. - Valec naležato
 Válec o průměru 3m a výšce/délce 15 m je položen naležato. Je do něj napuštěna voda, která sahá do výšky 60 cm pod osu válce. Kolik hektolitrů vody je ve válci?
Válec o průměru 3m a výšce/délce 15 m je položen naležato. Je do něj napuštěna voda, která sahá do výšky 60 cm pod osu válce. Kolik hektolitrů vody je ve válci? - Měděný drát
 Jakou hmotnost má 1000m měděného drátu o průměru 5mm, pokud měrná hustota p=8,8g/cm³?
Jakou hmotnost má 1000m měděného drátu o průměru 5mm, pokud měrná hustota p=8,8g/cm³? - Trojboký jehlan
 Vypočítejte objem a povrch pravidelného trojbokého jehlanu, jehož výška je stejná jako délka hrany podstavy 10 cm.
Vypočítejte objem a povrch pravidelného trojbokého jehlanu, jehož výška je stejná jako délka hrany podstavy 10 cm.
Máš příklad z matematiky, který jsi tady nenašel vyřešený? Pošli nám příklad a my Ti ho zkusíme vypočítat.
