Příklady na pravoúhlý trojúhelník - strana 26 z 84
Počet nalezených příkladů: 1676
- Usu
 Ze dvou míst A B na vodorovné rovině bylo pozorováno čelo mraku nad spojnicí obou míst pod výškovým úhlem 73°20' a 64°40'. Místa A B jsou od sebe vzdálená 2830 m. Jak vysoko je mrak?
Ze dvou míst A B na vodorovné rovině bylo pozorováno čelo mraku nad spojnicí obou míst pod výškovým úhlem 73°20' a 64°40'. Místa A B jsou od sebe vzdálená 2830 m. Jak vysoko je mrak? - Obvod a odvěsny
 Určete obvod pravoúhlého trojúhelníku, jestliže délka jedné odvěsny je 75% délky druhé odvěsny a jeho obsah je 24 cm².
Určete obvod pravoúhlého trojúhelníku, jestliže délka jedné odvěsny je 75% délky druhé odvěsny a jeho obsah je 24 cm². - Trojúhelník SUS
 Vypočítejte plochu a obvod trojúhelníku, pokud jeho dvě strany jsou dlouhé 20 m a 93 m a úhel nimi sevřený je 110°.
Vypočítejte plochu a obvod trojúhelníku, pokud jeho dvě strany jsou dlouhé 20 m a 93 m a úhel nimi sevřený je 110°. - Hrábě opřené o strom
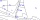 Ema hrabala listí v zahradě. Během oběda si hrábě dlouhé 170cm opřela o strom, přičemž horní konec hrábí sahal do výšky 90cm. Jak daleko od stromu byla spodní část hrábí? Výsledek uveďte v celých centimetrech.
Ema hrabala listí v zahradě. Během oběda si hrábě dlouhé 170cm opřela o strom, přičemž horní konec hrábí sahal do výšky 90cm. Jak daleko od stromu byla spodní část hrábí? Výsledek uveďte v celých centimetrech. - Trojúhelník PT + poměr
 V pravoúhlém trojúhelníku výška na přeponu je 4,8cm. Odvěsny jsou v poměru 4:3. Vypočítej obvod a obsah trojúhelníku
V pravoúhlém trojúhelníku výška na přeponu je 4,8cm. Odvěsny jsou v poměru 4:3. Vypočítej obvod a obsah trojúhelníku - Mám pravoúhlý
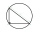 Mám pravoúhlý trojůhelník, délka přepony c 20 a znám jen poměr stran a:b = 2:1. nemůžu přijít na skutečnou délku těch odvěsen = sem už starší člobrda a mozek už mi nešlape na 100 % jako před lety na škole - tenkrát bych to určitě zvládl...
Mám pravoúhlý trojůhelník, délka přepony c 20 a znám jen poměr stran a:b = 2:1. nemůžu přijít na skutečnou délku těch odvěsen = sem už starší člobrda a mozek už mi nešlape na 100 % jako před lety na škole - tenkrát bych to určitě zvládl... - Výška domu
 Z vyhlídky na kostelní věži ve výšce 65m je vidět vrchol domu pod hloubkovým úhlem alfa = 45° a jeho spodek pod hloubkovým úhlem beta = 58°. Vypočtěte výšku domu a jeho vzdálenost od kostela.
Z vyhlídky na kostelní věži ve výšce 65m je vidět vrchol domu pod hloubkovým úhlem alfa = 45° a jeho spodek pod hloubkovým úhlem beta = 58°. Vypočtěte výšku domu a jeho vzdálenost od kostela. - Výška letadla
 V jaké výšce letí letadlo, které zaměřil radar pod výškovým úhlem 15°24‘ a přímá vzdálenost letadla od radaru 5545 m?
V jaké výšce letí letadlo, které zaměřil radar pod výškovým úhlem 15°24‘ a přímá vzdálenost letadla od radaru 5545 m? - Vrchol budovy
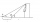 Z bodů A a B na vodorovném povrchu jsou úhly vyvýšenin horní části budovy 25° a 37°. Pokud | AB | = 57 m, vypočítejte, s přesností na metr, vzdálenosti horní části budovy od A a B, pokud jsou obě na stejné straně budovy
Z bodů A a B na vodorovném povrchu jsou úhly vyvýšenin horní části budovy 25° a 37°. Pokud | AB | = 57 m, vypočítejte, s přesností na metr, vzdálenosti horní části budovy od A a B, pokud jsou obě na stejné straně budovy - Řeka
 Z pozorovatelny 20 m vysoké a vzdálené 40 m od břehu řeky se jeví šířka řeky v zorném úhlu φ=18°. Vypočítejte šířku řeky.
Z pozorovatelny 20 m vysoké a vzdálené 40 m od břehu řeky se jeví šířka řeky v zorném úhlu φ=18°. Vypočítejte šířku řeky. - Centimetre - přepona
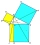 V pravoúhlém trojúhelníku má přepona délku 24cm. Pata výšky na přeponu ji dělí na dvě části v poměru 2:4. Jakou velikost v cm má výška na přeponu? Vypočítejte v centimetrech obvod tohoto pravoúhlého trojúhelníku.
V pravoúhlém trojúhelníku má přepona délku 24cm. Pata výšky na přeponu ji dělí na dvě části v poměru 2:4. Jakou velikost v cm má výška na přeponu? Vypočítejte v centimetrech obvod tohoto pravoúhlého trojúhelníku. - Z okna
 Z okna budovy ve výšce 7,5 m je vidět vrchol továrního komínu pod výškovým úhlem 76° 30′. Pata komínu je ze stejného místa vidět pod hloubkovým úhlem 5° 50′. Jak vysoký je komín?
Z okna budovy ve výšce 7,5 m je vidět vrchol továrního komínu pod výškovým úhlem 76° 30′. Pata komínu je ze stejného místa vidět pod hloubkovým úhlem 5° 50′. Jak vysoký je komín? - Graficky
 Řešte graficky následující úlohu. Rybářská loď vyjela z přístavu časně ráno a vydala se severním směrem. Po 12 km plavby změnila kurz a pokračovala 9 km na západ. Poté zakotvila a spustila sítě. Jak daleko byla od místa vyplutí?
Řešte graficky následující úlohu. Rybářská loď vyjela z přístavu časně ráno a vydala se severním směrem. Po 12 km plavby změnila kurz a pokračovala 9 km na západ. Poté zakotvila a spustila sítě. Jak daleko byla od místa vyplutí? - Rovnoramenný - lampy
 Podložky pod stolní lampy vyrábějí z bronzu ve tvaru rovnoramenného trojúhelníku. Kolik m² je zapotřebí pro 5 podložek, pokud ramena mají délku 24 cm a výška na základnu trojúhelníku má být 1,5 dm?
Podložky pod stolní lampy vyrábějí z bronzu ve tvaru rovnoramenného trojúhelníku. Kolik m² je zapotřebí pro 5 podložek, pokud ramena mají délku 24 cm a výška na základnu trojúhelníku má být 1,5 dm? - Stožár
 Stožár má 13 metrů dlouhý stín na svahu stoupajícím od sloupu sloupku ve směru úhlu stínu při úhlu 15°. Určete výšku stožáru, pokud je slunce nad obzorem (horizontem) v úhlu 33°. Použijte sinusovou větu.
Stožár má 13 metrů dlouhý stín na svahu stoupajícím od sloupu sloupku ve směru úhlu stínu při úhlu 15°. Určete výšku stožáru, pokud je slunce nad obzorem (horizontem) v úhlu 33°. Použijte sinusovou větu. - Lietadlo navigace
 Letadlo opustilo letiště a letí na západ 120 mil a pak 150 mil ve směru jiho-západ 42,47°. Jak daleko je letadlo od letiště? Zaokrouhlete na nejbližší míli.
Letadlo opustilo letiště a letí na západ 120 mil a pak 150 mil ve směru jiho-západ 42,47°. Jak daleko je letadlo od letiště? Zaokrouhlete na nejbližší míli. - Hloubkový úhel
 Určete výšku mraku nad hladinou jezera, vidíme-li ho z místa A pod výškovým úhlem 20° 57' az téhož místa A vidíme jeho obraz v jezeře pod hloubkovým úhlem 24° 12'. Pozorovací místo A je 115 m nad hladinou jezera.
Určete výšku mraku nad hladinou jezera, vidíme-li ho z místa A pod výškovým úhlem 20° 57' az téhož místa A vidíme jeho obraz v jezeře pod hloubkovým úhlem 24° 12'. Pozorovací místo A je 115 m nad hladinou jezera. - Maják
 Marcel (bod J) leží v trávě a vidí v zákrytu vrchol stanu (bod T) a za ním vrchol majáku (P). |TT'| = 1,2m, |PP'| = 36m, |JT'| = 5m. Marcel leží 15 m odbrehu moře (M). Vypočítejte vzdálenost majáku od břehu moře - |P'M| .
Marcel (bod J) leží v trávě a vidí v zákrytu vrchol stanu (bod T) a za ním vrchol majáku (P). |TT'| = 1,2m, |PP'| = 36m, |JT'| = 5m. Marcel leží 15 m odbrehu moře (M). Vypočítejte vzdálenost majáku od břehu moře - |P'M| . - Pozorovatelna
 Fotoaparát s úhlem záběru 120° byl umístěn horizontálně na vrchol pozorovatelny ve výšce 30m. Jaká je délka d úseku u základny věže, který nelze zachytit fotoaparátem?
Fotoaparát s úhlem záběru 120° byl umístěn horizontálně na vrchol pozorovatelny ve výšce 30m. Jaká je délka d úseku u základny věže, který nelze zachytit fotoaparátem? - Lyžař na kopci
 Lyžař se rozjíždí z kopce o délce l a úhlu sklonu 10˚. Potom přejde na vodorovný úsek trati, po kterém přejede až do zastavení stejnou délku l. Určete součinitel smykového tření mezi lyžemi a sněhem.
Lyžař se rozjíždí z kopce o délce l a úhlu sklonu 10˚. Potom přejde na vodorovný úsek trati, po kterém přejede až do zastavení stejnou délku l. Určete součinitel smykového tření mezi lyžemi a sněhem.
Máš úkol, který jsi tady nenašel vyřešen? Pošli nám úkol a my Ti ji zkusíme vypočítat. Řešení příkladů z matematiky.
