Ročník - slovní úlohy a příklady - strana 301 z 818
Počet nalezených příkladů: 16347
- Princip - 3CC
Podle jistého principu jsme rozdělili trojciferná přirozená čísla do dvou skupin: Do 1. skupiny patří například čísla: 158, 237, 689, 982, 731, 422, . .. Do 2. skupiny patří například čísla: 244, 385, 596, 897, … Odhalte princip rozdělení a zatřiďte násle - Koule
Osm malých vánočních koulí o poloměru 1 cm má stejný objem jako jedna velká vánoční koule. Co má větší povrch: osm malých koulí, nebo jedna velká koule? - Látka na kulové stínítko
Průměr kulového stínítka je 30 cm. Kolik m² látky potřebujeme k jeho zhotovení, musíme-li počítat 5% materiálu na sešití? - Na určitý
Na určitý výzkum na střední škole mají být z třídy s 30 žáky vyloskovaní 4 žáci. Vypočtěte počet všech možných výsledků losování a dále vypočítejte počet všech možných výsledků, pokud záleží na pořadí, v jakém žáci přijdou na pohovor. - Vlašský
Vlašský koláč frgal byl rozdělení na třetiny. Petr snědl jeden dílek. Jak velkou část koláče snědl a kolik koláče zbylo? - Kontrola zmetků
Ze série výrobků se má zkontrolovat 500 kusů, přičemž se provádí kontrola s opakováním. Výrobce garantuje při dané výrobě 2% zmetků. Určete pravděpodobnost, že mezi 500 kontrolovanými výrobky bude počet zmetků od 12 do 20. - Číslice Máme číslice 0,1,4,7, které se nemohou opakovat. Kolik trojmístných čísel z nich dokážeme zapsat? Můžeš si pomoci vypsáním všech čísel.
- Čtyřciferná čísla
Najděte čtyřciferná čísla, kde všechny číslice jsou různé. Pro čísla platí, že součet třetí a čtvrté číslice je dvakrát větší než součet prvních dvou čísel a součet první a čtvrté číslice je rovný součtu druhé a třetí číslice. Číslice 0 nesmí byt na první - Kvádr a kostka
Kvádr a kostka mají stejné objemy = 216 cm³. Kvádr má délky stran b = 4 cm, c = 9 cm. Mohou mít stejnou stranu a? - Šestá
Šestá třída jela na zájezd na Moravu. Každý z 26 žáků zaplatil 320 Kč a škola ještě doplácela celkem 3510 Kč. Jaká byla průměrná cena zájezdu na žáka? - Tatínek 6
Tatínek jel autem na služební cestu do místa vzdáleného 348 km. Na místo dorazil po čtyřech hodinách. Jakou průměrnou rychlostí se pohyboval? - Eva přečetla
Eva přečetla v pondělí 20 stránek dobrodružné knížky, v úterý 15, ve středu 19. Ve čtvrtek nečetla, ale v pátek přečetla 36 stran. Kolik stránek průměrně přečetla za den? - Bonbony v dóze
Vypočítejte kolik bonbonů se vejde do dózy tvaru 4-bokého hranolu s podstavou lichoběžníku o rozměrech základen 20 cm a 3,2 cm. Vzdálenost základen je 50 mm. Dóza je vysoká 32 cm a 1 bonbón zabere 2,5 cm³ objemu. - Obvod a šířka
Obvod a šířka obdélníku jsou v poměru 5:1. jeho obsah je 216cm². Jaká je jeho délka? - Zmetky
Při určité výrobě je pravděpodobnost výskytu zmetků 0,01. Vypočítejte, jaká bude pravděpodobnost, že mezi 100 vybranými výrobky bude více než 1 zmetek, pokud vybrané výrobky po kontrole vrátíme zpět do souboru. - Obvod půdorysu stánků
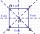Půdorys prodejních stánků se skládá ze čtverců a ve skutečnosti má obsah 48 m². Jaký obvod má půdorys těchto stánků? a. 34 m b. 36 m c. 40 m d. 44 m - Hmotnost 7
Hmotnost selete rostla po dobu čtyř měsíců pravidelně o pět kilogramů. Urči, v jakém poměru byla váha selete v jednotlivých měsících, jestliže prvního vážilo 35 kg. - Těsto 4
Těsto obsahuje vodu, mouku a cukr. Vodu a mouku v poměru 2:3, mouku a cukr v poměru 2:1. Urči poměr všech tří složek těsta. - Odvěsna trojúhelníku
Pravoúhlý trojúhelník má obsah 2304 cm² a jedna odvěsna je dlouhá 8 cm. Vyjádři a vypočítej druhou odvěsnu. - Rovnoběžné tětivy
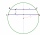V kružnici s průměrem 70 cm jsou narýsované dvě rovnoběžné tětivy tak, že střed kružnice leží mezi tětivami. Vypočítejte vzdálenost těchto tětiv, pokud jedna z nich má délku 42 cm a druhá 56 cm.
Máš příklad z matematiky, který jsi tady nenašel vyřešený? Pošli nám příklad a my Ti ho zkusíme vypočítat.
