Stereometrie - slovní úlohy a příklady - poslední strana

Počet nalezených příkladů: 2377

Seříznuty jehlan
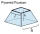Seříznutý jehlan se skládá ze čtvercové základny o délce 10 cm a vrchního čtverce o délce 7 cm. Výška seříznutého jehlanu je 6 cm. Vypočítejte povrch a objem.
Stínítko lampy
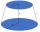
Stínítko lampy jako komolý má výšku 12 cm a horní a dolní průměr 10 cm a 20 cm. Jaká plocha materiálů je potřebná k pokrytí zakřiveného povrchu seříznutého okraje?
Úhlopříčky kvádru
Vypočtěte rozměry kvádru, pokud součet jeho hran je 19 cm. Velikost úhlopříčky těla je 13 cm a jeho objem je 144 cm³. Celková plocha je 192 cm².
Pyramida - jehlan
Seříznutý okraj pyramidy má 4 cm nahoře a 7 cm ve spodní části a je 6 cm vysoký. Vypočítejte objem seříznutého jehlanu.
Seříznutý 83654
Seříznutý kužel má průměry základny 10 cm, vrchol 6 cm a výšku 5 cm. Najděte délku boční strany (sklon) kužele.
Stan pro 11 osob
Kuželový stan pojme 11 osob. Každý člověk potřebuje 4 m² prostoru na zemi a 20 m³ vzduchu k dýchání. Najděte výšku stanu.
Vysvětlete 81386
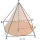Kužel má průměr x cm a výšku sklonu y cm. Čtvercový jehlan má délku strany základny x cm a výšku sklonu y cm. Který má větší povrch tělesa? Vysvětlete.
Dokonalý čtverec
Klasifikovali byste 324 jako dokonalý čtverec, dokonalou kostku, obojí nebo ani jedno? ...
Sousedních 83746
Pokud jsou plochy tří sousedních ploch kvádru 6, 10, 22, pak najděte objem kvádru.
Číselně 84347
Pokud jsou objem a povrch koule číselně stejné, najděte její poloměr.
Stan - polokoule
Mám stan ve tvaru kulové čepice (kulový odstavec). Předpokládejme, že chceme, aby objem byl 4 metry krychlové, aby se tam vyspali dva nebo tři lidé. Předpokládejme, že materiál tvořící kopuli desítky je dvakrát dražší na čtverec než materiál dotýkající se
Země a Měsíc
Průměr Měsíce je přibližně 1/4 průměru Země. Jaký zlomek objemu Země tvoří objem Měsíce?
Model z plastelíny
Pavel vytvoří kvádr z plastelíny se stranami 5 cm, 2 cm, 5 cm. Kolik takových kvádrů bude potřebovat k vytvoření kostky?
Kostka 4
Kostka s hranou 5 cm se rozřízne na kostky, každá s hranou 1 cm. Najděte poměr celkového povrchu jedné z malých kostek k celkové ploše velké kostky.
Zmenší + zvětší
Poloměr plného kruhového válce se zmenší o 20 % a jeho výška se zvětší o 10 %. Najděte procentuální změnu: a) objemu b) povrch zakřivené části pláště.
Dve koule v poměru
Povrch dvou koulí je v poměru 1:4. Najděte poměr jejich objemů.
Střed osy - kužel
Kužel o poloměru 10 cm je rozdělen na dvě části nakreslením roviny přes střed jeho osy, rovnoběžné s jeho základnou. Porovnejte objemy obou částí.

Máš příklad z matematiky, který jsi tady nenašel vyřešený? Pošli nám příklad a my Ti ho zkusíme vypočítat.