Stereometrie - slovní úlohy a příklady - strana 118 z 119
Počet nalezených příkladů: 2379
- Nádrž - akvarium
 Obdélníková nádrž o rozměrech 50 cm x 54 cm x 40 cm je z 3/5 naplněna vodou. Odstraní se 21,6 l vody. Jaký objem vody zůstává v nádrži? Odpověď uveďte v litrech.
Obdélníková nádrž o rozměrech 50 cm x 54 cm x 40 cm je z 3/5 naplněna vodou. Odstraní se 21,6 l vody. Jaký objem vody zůstává v nádrži? Odpověď uveďte v litrech. - Těleso
 Těleso má tvar kužele stojícího na polokouli, jehož oba poloměry se rovnají 1 cm a výška kužele se rovná jeho poloměru. Najděte objem tělesa.
Těleso má tvar kužele stojícího na polokouli, jehož oba poloměry se rovnají 1 cm a výška kužele se rovná jeho poloměru. Najděte objem tělesa. - Roztavení kostky
 Kolik válců o poloměru 20 cm a výšce 0,7 metru lze vytvořit roztavením kostky se stranou 2,2 metru?
Kolik válců o poloměru 20 cm a výšce 0,7 metru lze vytvořit roztavením kostky se stranou 2,2 metru? - Stínítko lampy
 Stínítko lampy má tvar seříznutého kužele s výškou sklonu 7 palců a poloměry základen 3 palce a 7 palců. Kolik materiálu se použije na jeho výrobu, je-li pro spoj povolen ¼ palce?
Stínítko lampy má tvar seříznutého kužele s výškou sklonu 7 palců a poloměry základen 3 palce a 7 palců. Kolik materiálu se použije na jeho výrobu, je-li pro spoj povolen ¼ palce? - Betonová roura
 Betonová trubka je dlouhá 1,0m. Jeho vnitřní a vnější průměr je 60 cm a 75 cm. Jaký objem betonu (metry kubické) je potřebný pro výrobu 25 ks trouby?
Betonová trubka je dlouhá 1,0m. Jeho vnitřní a vnější průměr je 60 cm a 75 cm. Jaký objem betonu (metry kubické) je potřebný pro výrobu 25 ks trouby? - Hemisféra - tobolka
 Tobolka léku je válec se dvěma hemisférami přilepenými na každém konci. Jeho délka je 14 mm a jeho průměr je 5 mm. Najděte její povrch.
Tobolka léku je válec se dvěma hemisférami přilepenými na každém konci. Jeho délka je 14 mm a jeho průměr je 5 mm. Najděte její povrch. - Vysoký válec
 Kolik dm² se rovná plocha 2 dm vysokého válce o průměru 1 dm?
Kolik dm² se rovná plocha 2 dm vysokého válce o průměru 1 dm? - Ferrum kostky
 Tři kostky železa, jejichž okraje jsou 6 cm, 8 cm a 10 cm, se roztaví a vytvarují do jedné kostky. Najděte hranu nové kostky.
Tři kostky železa, jejichž okraje jsou 6 cm, 8 cm a 10 cm, se roztaví a vytvarují do jedné kostky. Najděte hranu nové kostky. - Tavba dvou těles
 Dvě pevné koule o poloměrech 2 cm a 4 cm se roztaví a přetaví do kužele o výšce 8 cm. Najděte poloměr takto vytvořeného kužele.
Dvě pevné koule o poloměrech 2 cm a 4 cm se roztaví a přetaví do kužele o výšce 8 cm. Najděte poloměr takto vytvořeného kužele. - Roztavení
 Strany tří kovových kostek jsou 30 cm, 40 cm a 50 cm. Najděte stranu nové kostky vytvořené roztavením těchto kostek dohromady.
Strany tří kovových kostek jsou 30 cm, 40 cm a 50 cm. Najděte stranu nové kostky vytvořené roztavením těchto kostek dohromady. - Šestihran - výška
 Objem pravého pravidelného šestihranného hranolu je 187,2 kubických milimetrů. Úsečka, která má délku 2,6 milimetru, začíná ve středu šestiúhelníku a končí na jedné straně šestiúhelníku. 3 mm základna. Najděte výšku.
Objem pravého pravidelného šestihranného hranolu je 187,2 kubických milimetrů. Úsečka, která má délku 2,6 milimetru, začíná ve středu šestiúhelníku a končí na jedné straně šestiúhelníku. 3 mm základna. Najděte výšku. - Zdvojnásobení objemu
 Vytvořte si novou plechovku od nápoje, která zdvojnásobí objem použité původní plechovky. Rozměry dózy: průměr 6 cm a výška 10 cm. Máte zdvojnásobit objem s co nejmenším množstvím dodatečného hliníku potřebného pro novou plechovku. Jsou 3 možnosti: Možnos
Vytvořte si novou plechovku od nápoje, která zdvojnásobí objem použité původní plechovky. Rozměry dózy: průměr 6 cm a výška 10 cm. Máte zdvojnásobit objem s co nejmenším množstvím dodatečného hliníku potřebného pro novou plechovku. Jsou 3 možnosti: Možnos - Souprava - odměrka
 V odměrce je míra sklenice široká 6 cm. Souprava obsahuje také odměrku na 1 šálek a odměrku na šálek, přičemž obě jsou tvarem podobné odměrce na šálek. Najděte šířku: a) 1/2 šálku b) odměrka na 1 šálek c) odměrka 1/3 šálku.
V odměrce je míra sklenice široká 6 cm. Souprava obsahuje také odměrku na 1 šálek a odměrku na šálek, přičemž obě jsou tvarem podobné odměrce na šálek. Najděte šířku: a) 1/2 šálku b) odměrka na 1 šálek c) odměrka 1/3 šálku. - Výsledný kvádr
 Dvě kostky každá o objemu 125 cm³ jsou spojeny konci. Najděte povrch výsledného kvádru.
Dvě kostky každá o objemu 125 cm³ jsou spojeny konci. Najděte povrch výsledného kvádru. - Kubická krabice
 Krabice musí mít objem 108 ¾ kubických palců. Má-li být šířka krabice 7 ¼ palce a hloubka krabice 1 ¼ palce, jaká musí být výška krabice?
Krabice musí mít objem 108 ¾ kubických palců. Má-li být šířka krabice 7 ¼ palce a hloubka krabice 1 ¼ palce, jaká musí být výška krabice? - Velká nádrž
 Objem velké nádrže je 210 yd³. Je 2 2/5 yd široká a 2 4/5 yd vysoká. Jaká je délka nádrže?
Objem velké nádrže je 210 yd³. Je 2 2/5 yd široká a 2 4/5 yd vysoká. Jaká je délka nádrže? - Skladovací prostor
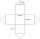 Frank navrhl síť pro skladovací prostor, který se chystá postavit z kovu. Design se skládá ze čtvercové základny a čtyř čtverečních stran plus čtyř trojúhelníkových částí, které tvoří střechu. Čtvercová základna 6 stop a čtyři čtvercové strany plus 4 stop
Frank navrhl síť pro skladovací prostor, který se chystá postavit z kovu. Design se skládá ze čtvercové základny a čtyř čtverečních stran plus čtyř trojúhelníkových částí, které tvoří střechu. Čtvercová základna 6 stop a čtyři čtvercové strany plus 4 stop - Povrch 5
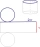 Povrch válce je 6140 cm² a poloměr je 25 cm. Jaká je jeho výška?
Povrch válce je 6140 cm² a poloměr je 25 cm. Jaká je jeho výška? - Hmotnost koule
 Jaká je hmotnost železné koule o průměru 1,0 dm? Hustota železa je 7870 kg/m³. .
Jaká je hmotnost železné koule o průměru 1,0 dm? Hustota železa je 7870 kg/m³. . - Centimetre - rotace
 Trojúhelník, jehož strany jsou 20 cm, 16 cm a 12 cm, se otáčí kolem své největší strany jako osy. Jaký je objem prostoru, který se generuje po úplné otáčce v kubických centimetrech?
Trojúhelník, jehož strany jsou 20 cm, 16 cm a 12 cm, se otáčí kolem své největší strany jako osy. Jaký je objem prostoru, který se generuje po úplné otáčce v kubických centimetrech?
Máš úkol, který jsi tady nenašel vyřešen? Pošli nám úkol a my Ti ji zkusíme vypočítat. Řešení příkladů z matematiky.
