Geometria - slovné úlohy a príklady - strana 20 z 37
Počet nájdených príkladov: 729
- Na obrázku 5
Na obrázku sú znázornené tri obce A, B, C a ich vzájomné vzdušné vzdialenosti. Nová priamočiara želežničná trať má byť postavená tak, aby zo všetkých obcí bolo k trati rovnako ďaleko a aby táto vzdialenosť bola najmenšia možná. Ako ďaleko budú od trate? a - Lin. závislosť
Zistite či vektory u=(-10; -6) a v=(30; 18) sú lineárne závislé. - Vzdialenosť priamok
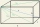Určite vzdialenosť priamok AE, CG v kvádra ABCDEFGH, ak je dané | AB | = 3cm, | AD | = 2 cm, | AE | = 4cm - Garáž
V garáži stojí pri stenách naproti sebe dve laty: jedna 2 metre dlhá a druhá 3 metre dlhá. Spadnú proti sebe a oprú sa o protiľahlé steny garáže obe laty sa prekríži vo výške 70 cm nad podlahou garáže. Ako široká je garáž? - Vpísaný trojuholník
Do kružnice je vpísaný trojuholník tak, že jeho vrcholy delia kružnicu na 3 oblúky. Dĺžky oblúkov sú v pomere 2:3:7. Urči vnútorné uhly trojuholníka. - Lineárny vzťah
P(x)=15x-(5x+10 000) určte x , aby P(x)=0 - Smernica
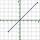Aká je smernica priamky definovaná rovnicou 5x +3y = -5? - Pozorovateľ 3
Pozorovateľ vidí vrcholce dvoch stromov v rovnakom uhle α. Od jedného stromu je vzdialený 9 m, od druhého 21 m. Stromy stoja na rovine. Aký vysoký je druhý strom, ak výška prvého je 6 m? Nezabudni, že oči stojaceho človeka sú približne 1,5 m nad zemou. - Náraz kamiónu
Vypočítajte výslednú rýchlosť oboch vozidiel po havárií auta s hmotnosťou m1 = 1,5 t idúceho rýchlosťou 100 km/h a kamiónu s hmotnosťou m2 = 40 ton idúceho rýchlosťou 90 km/h, ak sa jedná o čelnú haváriu. Vypočítajte preťaženie pôsob - Na kružnici
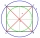Na kružnici s polomerom 10 cm a so stredom S sú dané body A, B, C tak, že stredový uhol ASB má 60 stupňov a stredový uhol ASC má 90 stupňov. Určte dĺžku oblúka kružnice a veľkosť posunutí AB a AC. - Severovýchod - kolobežky
Katka a Honza vyšli na kolobežkách v rovnakom čase. Katka išla rýchlosťou 4,5 km/30 min a Honza išiel rýchlosťou 4km/20 min. a) koľko m prešli za 2 min keď išli opačným smerom? b) koľko m prešli keď Honza išiel smerom na severovýchod a Katka smerom na juh - Ťažisko
Vypočítajte súradnice ťažiska T[x, y] trojuholníka ABC; A[30,29] B[-16,17] C[-25,-6] - Uhlopriečka lichobežníka
V lichobežníku ABCD sú dané dĺžky základní |AB| = 12 cm, |CD| = 8 cm. Bod S je priesečník uhlopriečok, pre ktorý platí |AS| = 6 cm. Vypočítaj dĺžku celej uhlopriečky AC. - Stred úsečky
Body P & Q patria do úsečky AB. Ak AB = a, AP = 2PQ = 2QB, nájdite vzdialenosť: medzi bodom A a stredom úsečky QB. - Vyznačené úsečky
Vyznač 4 rôzne body O, P, R. S. Vyznač úsečky OP, OR, OS. Vyznačené úsečky zmeraj. - V trojuholniku 6
V trojuholníku tma platí, že dĺžka strán t =5cm, m =3,5cm, a=6,2cm . Iný s ním podobný trojuholník má dĺžky strán 6,65cm 11,78cm 9,5cm. Urč koeficient podobnosti týchto trojuholníkov. Priraď tieto dĺžky k stranám trojuholníka NOC, tak aby platilo TMA~NOC - Obvodový uhol
Vrcholy trojuholníka ΔABC vpísaného do kružnice ju delia na oblúky v pomere 10:4:6. Určte veľkosti vnútorných uhlov ΔABC. - Medzi
Medzi 3 stĺpiky je natiahnuté oceľové lanko. Výška prvého stĺpa je 4 m, výška druhého je 3,5m. Vzdialenosť prvých dvoch stĺpikov je 2,5m, vzdialenosť druhího a tretieho je 5m. Päty všetkých troch stĺpikov stojí v jednej priamke. Aká je výška tretieho stĺp - Guľa
Získajte rovnicu guľovej plochy so stredom na čiare 3x + 2z = 0 = 4x-5y a prechádza bodmi (0, -2, -4) a (2, -1,1). - Východ-sever
Osobné auto vyšlo o 7,00 hod. A smerovalo na východ rýchlosťou 60km/h. Z toho istého miesta vyšiel motocyklista a smeroval na sever rýchlosťou 40 km/h. Aká bude ich vzdušná vzdialenosť o desiatej hodine?
Máš úlohu, ktorú si tu nenašiel vyriešenú? Pošli nám túto úlohu a my Ti ju skúsime vypočítať. Riešime príklady a úlohy z matematiky. Nielen domáce.
