Geometria - slovné úlohy a príklady - strana 28 z 37
Počet nájdených príkladov: 733
- Rýchlosť veslice
 Veslice plávajúce po rieke urazila vzdialenosť 120 m pri plavbe po prúde za 12 s, pri plavbe proti prúdu za 24 s. Určite veľkosť rýchlosti veslice vzhľadom na vodu a veľkosť rýchlosti prúdu v rieke. Obe rýchlosti sú konštantné.
Veslice plávajúce po rieke urazila vzdialenosť 120 m pri plavbe po prúde za 12 s, pri plavbe proti prúdu za 24 s. Určite veľkosť rýchlosti veslice vzhľadom na vodu a veľkosť rýchlosti prúdu v rieke. Obe rýchlosti sú konštantné. - Polohový vektor
 Polohový vektor hmotného bodu, ktorý sa pohybuje v rovine, je možné v zavedenej vzťažnej sústave vyjadriť vzťahom: r(t) = (6t²+ 4t ; 3t + 1) kde t je čas v sekundách a súradnice vektora sú v metroch. Vypočítajte: a) aká je poloha hmotného bodu v čase t =
Polohový vektor hmotného bodu, ktorý sa pohybuje v rovine, je možné v zavedenej vzťažnej sústave vyjadriť vzťahom: r(t) = (6t²+ 4t ; 3t + 1) kde t je čas v sekundách a súradnice vektora sú v metroch. Vypočítajte: a) aká je poloha hmotného bodu v čase t = - Kružnica
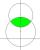 Kružnica k má stred S[-3; -10] a najväčšia tetiva má dĺžku 12. Koľko spoločných bodov má kružnica so súradnicovými osami?
Kružnica k má stred S[-3; -10] a najväčšia tetiva má dĺžku 12. Koľko spoločných bodov má kružnica so súradnicovými osami? - Lichobežník MO-5-Z8
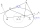
 Lichobežník ABCD je úsečkou CE rozdelený na trojuholník a rovnobežník, viď obrázok. Bod F je stredom úsečky CE, priamka DF prechádza stredom úsečky BE a obsah trojuholníka CDE je 3 cm². Určte obsah lichobežníka ABCD.
Lichobežník ABCD je úsečkou CE rozdelený na trojuholník a rovnobežník, viď obrázok. Bod F je stredom úsečky CE, priamka DF prechádza stredom úsečky BE a obsah trojuholníka CDE je 3 cm². Určte obsah lichobežníka ABCD. - Dotyčnica elipsy
 Nájdite dotyčnicu elipsy 9 x² + 16 y² = 144, ktorá má sklon (smernicu) k = -1
Nájdite dotyčnicu elipsy 9 x² + 16 y² = 144, ktorá má sklon (smernicu) k = -1 - Vektory 5
 Polohový vektor hmotného bodu, ktorý sa pohybuje v rovine, je možné v zavedenej vzťažnej sústave vyjadriť vzťahom: r(t) = (2t + 3t²; 6t + 3), kde t je čas v sekundách a súradnice vektora sú v metroch. Vypočítajte: a) aká je poloha hmotného bodu v čase t =
Polohový vektor hmotného bodu, ktorý sa pohybuje v rovine, je možné v zavedenej vzťažnej sústave vyjadriť vzťahom: r(t) = (2t + 3t²; 6t + 3), kde t je čas v sekundách a súradnice vektora sú v metroch. Vypočítajte: a) aká je poloha hmotného bodu v čase t = - V rovine 2
 V rovine je 10 ľubovoľných bodov. Koľko najviac kružníc je nimi určených?
V rovine je 10 ľubovoľných bodov. Koľko najviac kružníc je nimi určených? - Nádoba
 Uzavretá nádoba v tvare kužeľa stojaca na svojej podstave je naplnená vodou tak, že hladina sa nachádza 8 cm od vrcholu. Po otočení nádoby o 180 stupňov - stojí na vrchole - je hladina vzdialená 2 cm od podstavy. Ako vysoká nádoba je?
Uzavretá nádoba v tvare kužeľa stojaca na svojej podstave je naplnená vodou tak, že hladina sa nachádza 8 cm od vrcholu. Po otočení nádoby o 180 stupňov - stojí na vrchole - je hladina vzdialená 2 cm od podstavy. Ako vysoká nádoba je? - Trojuholník - mapa
 Určte merítko mapy, ak je les tvaru trojuholníka s rozmermi 1,6 km, 2,4 km a 2,7 km na mape zakreslený ako trojuholník so stranami dĺžok 32 mm, 48 mm a 54 mm.
Určte merítko mapy, ak je les tvaru trojuholníka s rozmermi 1,6 km, 2,4 km a 2,7 km na mape zakreslený ako trojuholník so stranami dĺžok 32 mm, 48 mm a 54 mm. - Podobnosť
 Sú dva pravouhlé trojuholníky navzájom podobné, ak prvý má ostrý uhol 50° a druhý má ostrý uhol 40°?
Sú dva pravouhlé trojuholníky navzájom podobné, ak prvý má ostrý uhol 50° a druhý má ostrý uhol 40°? - Trojuholník
 Trojuholník je daný tromi vrcholmi: A [0,0] B [-4,2] C [-6,0] Vypočítajte V (priesečník výšok), T (ťažisko), O - stred kružnice opísanej
Trojuholník je daný tromi vrcholmi: A [0,0] B [-4,2] C [-6,0] Vypočítajte V (priesečník výšok), T (ťažisko), O - stred kružnice opísanej - Napíšte 8
 Napíšte rovnicu dotyčnice hyperboly 9x²−4y²=36 v bode T =[t1,4].
Napíšte rovnicu dotyčnice hyperboly 9x²−4y²=36 v bode T =[t1,4]. - Polohový 2
 Polohový vektor hmotného bodu, ktorý sa pohybuje v rovine, je možné v zavedenej vzťažnej sústave vyjadriť vzťahom: r(t) = (1 + 5t + 2t² ; 3t + 1), kde t je čas v sekundách a súradnice vektora sú v metroch. Vypočítajte: a) aká je poloha hmotného bodu v čas
Polohový vektor hmotného bodu, ktorý sa pohybuje v rovine, je možné v zavedenej vzťažnej sústave vyjadriť vzťahom: r(t) = (1 + 5t + 2t² ; 3t + 1), kde t je čas v sekundách a súradnice vektora sú v metroch. Vypočítajte: a) aká je poloha hmotného bodu v čas - Štvorec ABCD
 Zostrojte štvorec ABCD so stredom S [3,2] a stranou a = 4cm. Vrchol A leží na osi x. Zostrojte jeho obraz v posunutí danom orientovanou úsečkou SS'; S` [-1, - 4].
Zostrojte štvorec ABCD so stredom S [3,2] a stranou a = 4cm. Vrchol A leží na osi x. Zostrojte jeho obraz v posunutí danom orientovanou úsečkou SS'; S` [-1, - 4]. - Kružnice
 Dokážte, že rovnice k1 a k2 predstavujú kružnice. Napíšte rovnicu priamky, ktorá prechádza stredmi týchto kružníc. k1: x²+y²+2x+4y+1=0 k2: x²+y²-8x+6y+9=0
Dokážte, že rovnice k1 a k2 predstavujú kružnice. Napíšte rovnicu priamky, ktorá prechádza stredmi týchto kružníc. k1: x²+y²+2x+4y+1=0 k2: x²+y²-8x+6y+9=0 - Zrezaný kúžeľ
 Horný a dolný polomer zrezaného pravého kruhového kužeľa je 8 cm a 32 cm. Ak je výška zrezaného okraja 10 cm, ako ďaleko od spodnej základne musí byť vytvorená rovina rezu, aby sa vytvorili dva podobné zrezané kužeľe?
Horný a dolný polomer zrezaného pravého kruhového kužeľa je 8 cm a 32 cm. Ak je výška zrezaného okraja 10 cm, ako ďaleko od spodnej základne musí byť vytvorená rovina rezu, aby sa vytvorili dva podobné zrezané kužeľe? - Plocha trojuholníka
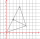 Trojuholník má vrcholy A(-1,-2), B(2,2) a C(-1,4). Aká je plocha △ABCv štvorcových súradnicových jednotkách?
Trojuholník má vrcholy A(-1,-2), B(2,2) a C(-1,4). Aká je plocha △ABCv štvorcových súradnicových jednotkách? - Zostrojenie trojuholníka
 Vrcholy trojuholníka ABC ležia na kružnici tak, že ju delia na tri diely v pomere 1:2:3. Zostroj tento trojuholník.
Vrcholy trojuholníka ABC ležia na kružnici tak, že ju delia na tri diely v pomere 1:2:3. Zostroj tento trojuholník. - Zostrojte 8
 Zostrojte trojuholník KLM kde strana k má 6,7cm; ťažnica na stranu k je 4,1cm a uhol LKM má 63 stupňov. Napíšte postup konštrukcie.
Zostrojte trojuholník KLM kde strana k má 6,7cm; ťažnica na stranu k je 4,1cm a uhol LKM má 63 stupňov. Napíšte postup konštrukcie. - Z9 – I – 2 MO 2018
 V rovnostrannom trojuholníku ABC je K stredom strany AB, bod L leží v tretine strany BC bližšie bodu C a bod M leží v tretine strany AC bližšie bodu A. Určte, akú časť obsahu trojuholníka ABC zaberá trojuholník KLM.
V rovnostrannom trojuholníku ABC je K stredom strany AB, bod L leží v tretine strany BC bližšie bodu C a bod M leží v tretine strany AC bližšie bodu A. Určte, akú časť obsahu trojuholníka ABC zaberá trojuholník KLM.
Máš úlohu, ktorú si tu nenašiel vyriešenú? Pošli nám túto úlohu a my Ti ju skúsime vypočítať. Riešime príklady a úlohy z matematiky. Nielen domáce.
