Stereometria - slovné úlohy a príklady - strana 111 z 119
Počet nájdených príkladov: 2367
- Pilier
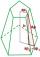Určite objem piliera tvaru pravidelného štvorbokého zrezaného ihlana, ak jeho štvorcové postavy majú strany a = 19, b = 30 a výška piliera je v = 42. - Hrany v pomere
Povrch kvádra je 5 632 m². Dĺžky hrán sú v pomere 1 : 2 : 3. Vypočítajte objem kvádra. - Plavák
0,5 m guľovitý plavák je používaný ako umiestnenie ochrannej značky pre kotviace rybárske lode. Pláva v slanej vode. Nájdite hĺbku, v ktorej plavák klesá v prípade, že materiál, z ktorého je vyrobený váži 8 kilogramov na meter kubický a slaná voda hmotnos - Súčiastka
Súčiastka tvaru zrezaného kúžeľa s polomermi podstáv 4 cm a 22 cm sa má pretaviť na súčiastku tvaru valca rovnakej výšky ako pôvodná súčiastka. Aký polomer podstavy bude mať nová súčiastka? - Kužel - rez
Rotačný kužeľ s výškou 25 cm a objemom 15386 cm³ je v tretine výšky (merané zospodu) rozrezaný rovinou rovnobežnou s podstavou. Určte polomer a obvod kruhového rezu. - Rez ihlana
Pravidelný ihlan so štvorcovou podstavou rozrežeme rovinou rovnobežnou s podstavou na dve časti (pozrite obrázok). Objem vzniknutého menšieho ihlana tvorí 20 % objemu pôvodného ihlana. Podstava vzniknutého menšieho ihlana má obsah 10 cm². Určte v centimet - 4BH - podstavná hrana
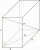Je daný pravidelný štvorboký hranol ABCDEFGH s podstavnou hranou AB dĺžky 8 cm a výškou 6 cm. Bod M je stred hrany AE. Určite vzdialenosť bodu M od roviny BDH.
- Poklad
Skauti majú stan v tvare pravidelného štvorbokého ihlanu so stranou podstavy 4 m a výške 3 m. Do stanu potrebujú schovať valcovú nádobu s tajným pokladom. Určte polomer r (a výšku h) nádoby tak, aby mohli schovať čo nejobjemnější poklad. - Bude plávať?
Bude vo vode plávať dutá železná guľa s vonkajším priemerom d1 = 20cm a vnútorným priemerom d2 = 19cm? Hustota železa je 7,8g/cm³. (Návod: Vypočítajte priemernú hustotu gule a porovnajte s hustotou vody. ) - Hektolitre v bazéne
Povrch vody v bazéne tvorí obdĺžnik s dĺžkou 50 metrov a šírkou 12 metrov. Hĺbka vody stúpa rovnomerne od 1 metra na jednom konci bazéna do 3 metrov na druhom konci bazéna (dlhšie strany). Určite množstvo vody v bazéne v hektolitroch. - Do rovnostranného 2
Do rovnostranného rotačného valca je vpísaná guľa ( dotýka sa podstáv i plášťa). Dokážte, že valec má objem i povrch o polovicu väčší než guľa do neho vpísaná. - Tetraéder
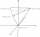Určte polohu ťažiska sústavy štyroch hmotných bodov, ktoré majú hmotnosti, m1, m2=2m1, m3=3m1 a m4=4m1, ak ležia vo vrcholoch rovnorameného tetraédra. (vo všetkých pripadoch medzi susednými hmotnymi bodmi je vzd - Do nádoby 2
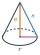Do nádoby tvaru rovnostranného kužeľa, ktorého podstava má polomer r = 6 cm nalejeme toľko vody, že sa naplní jedna tretina objemu kužeľa. Do akej výšky bude siahať voda, ak kužeľ obrátime hore dnom? - Mierka
Na výkrese je nakreslený valec v mierke 2:1. Koľko krát je objem tohto valca v skutočnosti menší? - Kral sa
Kráľ sa nevie rozhodnúť, ako má čo najspravodlivejšie rozdeliť dvom synom 4 kocky čistého zlata, ktoré majú hranu dĺžky 3cm, 4cm, 5cm, 6cm . Navrhnite riešenie tak, aby sa nemuseli kocky rezať.
- Nádoba
Uzavretá nádoba v tvare kužeľa stojaca na svojej podstave je naplnená vodou tak, že hladina sa nachádza 8 cm od vrcholu. Po otočení nádoby o 180 stupňov - stojí na vrchole - je hladina vzdialená 2 cm od podstavy. Ako vysoká nádoba je? - Osem kvádrov
Dana mala za úlohu uložiť osem kvádrov podľa týchto pravidiel: 1. Medzi dvoma červenými kvádre musí byť jeden inej farby. 2. Medzi dvoma modrými musia byť dva iné farby. 3. Medzi dvoma zelenými musia byť tri inej farby. 4. Medzi dvoma žltými kvádre musia - Vektor
Vypočítajte veľkosť vektora v&; 8407; = (9,75, 6,75, -6,5, -3,75, 2) - Pologuľa
Nádoba tvaru pologule je úplne naplnená vodou. Aký polomer má nádoba, keď z nej pri naklonení o 30 stupňov vytečie 10 l vody? - Priesečník
Je daný pravidelný štvorboký ihlan ABCDV, vo vnútri jeho hrany AV je bod M, na preslúženej úsečke DC za bod C je bod N. Zostrojte priesečnicu roviny MNV s rovinou BCV a priesečník priamky MN a roviny BCV.
Máš príklad, nad ktorým si premýšľaš aspoň 10 minút? Pošli nám príklad a my Ti ho skúsime vypočítať.
