Tupý úhel
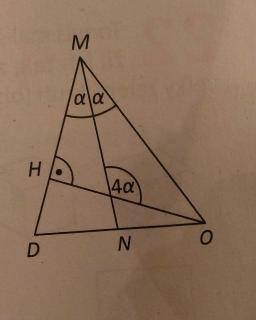
Úsečka OH je výškou trojúhelníku DOM, úsečka MN leží na ose úhlu při vrcholu M. Tupý úhel mezi úsečkami OH a MN je čtyři krát větší než úhel DMN. Jakou velikost má úhel DMO? (přikládám i obrázek)
Správná odpověď:
Tipy na související online kalkulačky
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
Jednotky fyzikálních veličin:
Úroveň náročnosti úkolu:
Související a podobné příklady:
- Trojúhelníku
Trojúhelníku ABC je velikost vnitřního úhlu α o 12° menší než úhel β a úhel γ je 4 krát větší než úhel α. Jakou velikost mají tyto vnitřní úhly v trojúhelníku? - Sousední úhly
Jeden ze sousedních úhlů je 3 krát větší než druhý. Jakou má velikost větší ze sousedních úhlů? - Čtyřúhelníku 82395
Body ABC leží na kružnici k(S, r) tak, že úhel u B je tupý. Jak velký musí být úhel u vrcholu B čtyřúhelníku SCBA, aby byl tento úhel třikrát větší než vnitřní úhel ASC téhož čtyřúhelníku? - V rovnoramenném 2
V rovnoramenném trojúhelníku je velikost úhlu při hlavním vrcholu o 20° menší než dvojnásobná velikost úhlu při základně. Jaké jsou vnitřní úhly trojúhelníku?
- Uhly
Vnější úhel trojúhelníku ABC při vrcholu A je 137°36'. Vnější úhel při vrcholu B je 102°36'. Jakou velikost má vnitřní úhel při vrcholu C? - Úhel při 3
Úhel při základě rovnorameného trojúhelníku je o 18° větší než úhel při hlavním vrcolu. Vypočtěte velikost vnitřních úhlů - Pravoúhlý
V trojúhelníku s pravím úhlem u vrcholu C je úhel alfa o 24 stupnu menší než uhel beta určete velikost úhlů trojúhelníka.
